[TOC]
最简单的线性回归模型可以用如下公式表示:
\[y(\mathrm{x},\mathrm{w}) = w_0+w_1x_1+\dots+w_Mx_D\]其中, $\mathrm{x}=(x_1,\dots,x_D)^\mathsf{T}$ 为输入的 $D$ 维特征向量,需要求解参数向量(也称作权重,或者回归系数) $\mathrm{w}=(w_0,\dots,w_D)$ ,这种模型是多元一次方程,为了扩展到多项式模型,一般的线性模型用如下公式表示:
\[y(\mathrm{x},\mathrm{w}) = w_0+\sum_{j=1}^{M-1}w_j \phi_j(\mathrm{x})\]其中, $\phi_j(x)$ 称作 基函数 (basis function), $w_0$ 是一个固定长度的偏移量,称作 偏差 (bias)参数。定义 $\phi_0(x)=1$ ,可以得到更紧凑的表示方式:
\[y(\mathrm{x},\mathrm{w}) = \sum_{j=0}^{M-1} w_j\phi_j(\mathrm{x}) = \mathrm{w}^\mathsf{T}\mathrm{\phi}(\mathrm{x})\]其中, $\mathrm{w}=(w_0,\dots,w_{M-1})^\mathsf{T}$ 和 $\mathrm{\phi}=(\phi_0,\dots,\phi_{M-1})^\mathsf{T}$ 。
注:这里使用PRML里的符号 $\phi(x)$ 来表示假设 $h(x)$ , $w$ 表示参数 $\theta$ 。
基函数
基函数可以是一个高斯函数:
\[\phi_j(x) = \exp \left(-\frac{(x-\mu_j)^2}{2s^2}\right)\]也可以是sigmoid函数,此时相当于特化成逻辑回归(logistic regression)问题,互联网行业中广告CTR预估常用该模型:
\[\sigma(a) = \frac{1}{1+e^{-a}} \\ \phi_j(x) = \sigma \left(\frac{x-\mu_j}{s}\right)\]普通最小二乘法
根据之前最大似然的博文,可知最大似然假设等价于最小化平方损失函数。定义平方损失函数:
\[L(\mathrm{w}) = \frac{1}{2} \sum_{i=1}^N (y_i - \mathrm{w}^\mathsf{T} \phi(\mathrm{x}_i))^2\]其中, $N$ 表示输入的训练数据的数目。上式用矩阵表示如下:
\[L(\mathrm{w}) = (y-\Phi \mathrm{w})^\mathsf{T} (y - \Phi \mathrm{w})\]其中, $\Phi$ 是一个 $N \times M$ 的矩阵,其物理意义是 $N$ 组 $M$ 维的训练数据:
\[\Phi = \begin{pmatrix} \phi_0(\mathrm{x}_1) & \phi_1(\mathrm{x}_1) & \cdots & \phi_{M-1}(\mathrm{x}_1) \\ \phi_0(\mathrm{x}_2) & \phi_1(\mathrm{x}_2) & \cdots & \phi_{M-1}(\mathrm{x}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_0(\mathrm{x}_N) & \phi_1(\mathrm{x}_N) & \cdots & \phi_{M-1}(\mathrm{x}_N) \\ \end{pmatrix}\]如果对 $\mathrm{w}$ 求导,并使得其梯度为0,求解如下方程:
\[\Phi^\mathsf{T}(y - \Phi \mathrm{w}) = 0\]解到 $\mathrm{w}$ 如下:
\[\hat{\mathrm{w}} = (\Phi^\mathsf{T}\Phi)^{-1}\Phi^\mathsf{T} y\]其中, $\hat{\mathrm{w}}$ 是当前可以估计出的 $\mathrm{w}$ 的最优解。注意,由于该方法需要对矩阵求逆,因此该方法只有在逆矩阵存在时适用。此外,我们需要把所有的训练数据都放在矩阵里做运算,所以数据规模有一定限制,一般适用于维数不高数据量不大的情况。通常情况下还是使用梯度下降法计算回归系数。
数学描述
微积分角度来讲,最小二乘法是采用非迭代法,针对代价函数求导数而得出全局极值,进而对所给定参数进行估算。
计算数学角度来讲,最小二乘法的本质上是一个线性优化问题,试图找到一个最优解。
线性代数角度来讲,最小二乘法是求解线性方程组,当方程个数大于未知量个数,其方程本身无解,而最小二乘法则试图找到最优残差。
几何角度来讲,最小二乘法中的几何意义是高维空间中的一个向量在低维子空间的投影。
概率论角度来讲,如果数据的观测误差是/或者满足高斯分布,则最小二乘解就是使得观测数据出现概率最大的解,即最大似然估计(利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值)。
梯度下降法
数学中对向量梯度的定义如下:
\[\nabla_{\mathrm{w}} L(\mathrm{w}) = \begin{bmatrix} \frac{\partial}{\partial w_0}L(\mathrm{w}) \\ \vdots \\ \frac{\partial}{\partial w_n}L(\mathrm{w}) \\ \end{bmatrix} \\\]梯度下降法的主要思想是:先估计一个初始的参数 $\mathrm{w}$ ,然后改变参数 $\mathrm{w}$ 使得损失函数 $L(\mathrm{w})$ 逐步向梯度减小最快的方向迭代。
\[\mathrm{w}_j := \mathrm{w}_j - \alpha\nabla_{\mathrm{w}} L(\mathrm{w})\]其中, $\alpha$ 表示步长, $j=0,\dots,n$ ,经过 $n$ 步迭代,最终收敛到一个极值(有可能只是局部极大或者极小值)。
求解损失函数 $L(w)$ 的梯度即对各参数求偏导:
\[\begin{align} \frac{\partial}{\partial w_j}L(\mathrm{w}) &= \frac{\partial}{\partial w_j} \frac{(y - \phi(x))^2}{2} \\ &= (y - \phi(x))x_j \end{align}\]得到梯度下降的算法流程:
\[\begin{align} &\textrm{Repeat until convergence }\{ \\ &\quad \mathrm{w}_j := \mathrm{w}_j - \alpha \sum_{i=1}^N(y^{(i)} - \phi(x^{(i)}))x_j^{(i)} \quad \textrm{ (for every j).} \\ &\} \end{align}\]局部加权线性回归
LWLR主要为了解决LR欠拟合问题。
\[\hat{\mathrm{w}} = (\Phi^\mathsf{T}W\Phi)^{-1}\Phi^\mathsf{T}W y\]其中, $W$ 是一个矩阵,用来给每个数据点赋权重,具体是使用核函数来赋值。常用的核函数是高斯核:
\[W(i,i) = \exp \left(\frac{|x^{(i)} - x|}{-2 k^2}\right)\]其中, $k$ 是交由用户调整的一个参数。
岭回归
最小二乘法是一种无偏估计。当 $\Phi$ 不满足列满秩,或者某些列之间的线性相关性比较大时, $\Phi^\mathsf{T}\Phi$ 的行列式接近于0,即 $\Phi^\mathsf{T}\Phi$ 接近于奇异,计算 $(\Phi^\mathsf{T}\Phi)^{-1}$ 时误差会很大。此时,传统的最小二乘法缺乏稳定性与可靠性。
岭回归是对最小二乘法的一种补充,它损失了无偏性,来换取高的数值稳定性,从而得到较高的计算精度。具体做法是将 $\Phi^\mathsf{T}\Phi$ 对角线元素都加上 $k$ ,可以使得矩阵为奇异的风险大大降低:
\[\hat{\mathrm{w}} = (\Phi^\mathsf{T}\Phi + k \mathbf{I})^{-1}\Phi^\mathsf{T} y\]一个python的示例
首先,在ipython里启动numpy和matplotlib环境。假设我们的目标函数如下:
# 目标函数 y = w0 + w1 * x^2
def func(x, p):
w0, w1 = p
return w0 + w1 * (x**2)
定义损失函数(该函数返回值会被leastsq平方,所以这里返回差值即可)
def loss(p, y, x):
return y - func(x, p)
生成带噪声的训练数据
x = linspace(-10, 10)
w0, w1 = 10, -0.5 # 实际的参数值
y0 = func(x, (w0, w1))
y1 = y0 + 2 * randn(len(x)) # 模拟带噪声的训练数据
设置初始的回归系数
p0 = (0, 0)
调用scipy.optimize.leastsq函数计算回归系数
p, ret = leastsq(loss, p0, args=(y1, x))
利用matplotlib绘制出结果
plot(x, y1, label=u"带噪声的数据")
plot(x, func(x, p), label=u"拟合函数")
legend()
show()
得到如下示意图
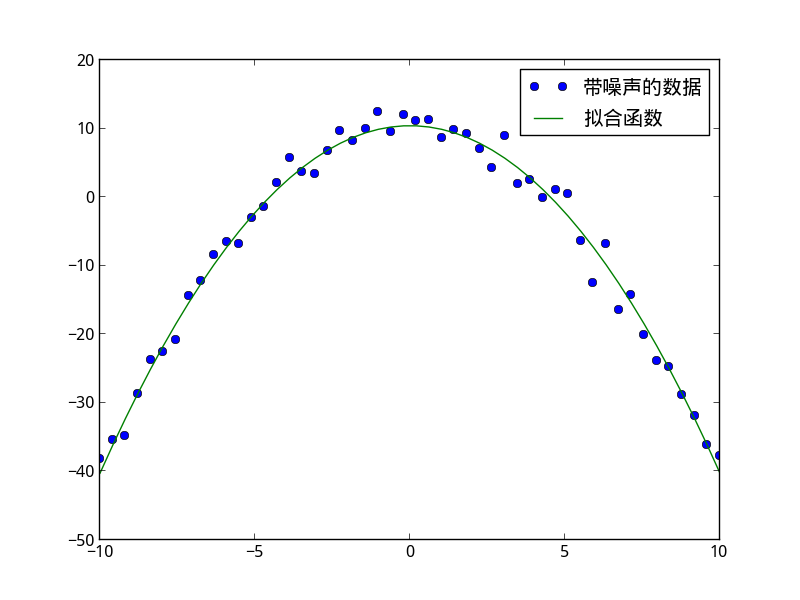
参考
- PRML 3. Linear Models For Regression
- ML in Action 8. Predicting numeric values: regression
- Stanford cs229 Lecture notes 1