$\newcommand{\x}{\mathbf{x}}$
第一次接触CRF的确很难理解,因为《统计自然语言处理》这本书上讲CRF一共就两页多一点,还有些概念没有铺垫就扔出来,所以读完依旧懵逼……
后来反复结合上下篇章,以及CRF论文,才明白CRF有很多的背景知识需要了解,如:马尔可夫网络、马尔可夫性(Markov property)、团(clique)、PGM中无向图建模方法、团的势能函数(clique potential function)、判别模型等知识,以及CRF和HMM、MEMM的关系等,所以这里写一篇blog给自己整理一下思路。
马尔可夫网络
- 马尔可夫网络
- 也称作马尔可夫随机场(Markov random field, MRF),是一组有 马尔可夫性质 的随机变量的联合概率分布模型,它由一个 无向图 $G$和定义于$G$上的 势函数 组成。
无向图$G=(V, E)$,每个顶点$x_i\in V$ 表示集合$X$上的一个随机变量,每条边$\brace{ x_i,x_j} \in E \, (i\neq j)$ 表示直接相连的两个随机变量$x_i$和$x_j$之间的依赖关系。
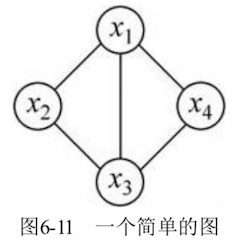
- 团
- 无向图中的完全连通子图。比如,$\x_C=\brace{ x_1,x_2}$ 表示团$C$中的所有结点。
- 极大团
- 如果团中加入任意一个结点均不再是团。比如,$\brace{ x_1,x_2,x_3}$ 和 $\brace{ x_1,x_3,x_4}$ 都是极大团。
回忆一下贝叶斯网络和HMM的建模方法,采用条件概率来计算整个图的联合概率。但在无向图中,不用条件概率密度建模,而采用团势能(clique potentials)。
- 团势能
- 也称作团势能函数 或 势函数,是定义在团上的非负实函数。一般定义为 $\phi(\x_C)=\exp(-E(\x_C))$,其中,$E(\x_C)$称作$\x_C$的能量函数(energy function)。
- Hammersley-Clifford 定理
- 对$n$个随机变量$\brace{ x_1,x_2,\cdots,x_n}$组成的马尔可夫网络$G$,如果$C=\brace{ C_1,C_2,\cdots,C_K}$是$G$上极大团的集合,则$G$的联合分布可以用$C$的势函数$\phi(\x_c)$进行建模(因子化):
\[p(x_1,x_2,\cdots,x_n) = \frac1Z \prod_{i=1}^K \phi_i(\x_{C_i})\]
其中,$Z$是一个归一化常量,称为划分函数(partition function):
\[Z = \sum_{x_1,\cdots,x_n} \prod_{i=1}^K \phi_i(\x_{C_i})\]
条件随机场
类似于HMM,CRF同样有两个序列(解决序列标注问题,比如分词、NER问题):
- 观测序列 $X$,如已经分好的词序列
- 标注序列 $Y$,如需要标注的实体序列
CRF通过直接定义条件概率$P(Y\vert X)$,而不是联合概率建模。
CRF定义:在MRF基础上,需要观察序列$X$为条件时,每一个随机变量$Y$都满足以下马尔可夫特性:
\[p(Y_v|X,Y_w, w\neq v) = p(Y_v|X,Y_w,w\sim v)\]其中,$w\sim v$表示两个结点在图$G$里是邻接结点。意思就是某点的条件概率可以只用它的邻接结点来表示。
【注】马尔可夫性质包括pairwise/local/global三种逐渐增强的性质,简单来说,在无向图中,给定所有其他结点/邻接结点/分离集合结点的条件下,两部分不相邻的结点(随机变量)条件独立。
一般都使用线性链式CRF,结构如图:
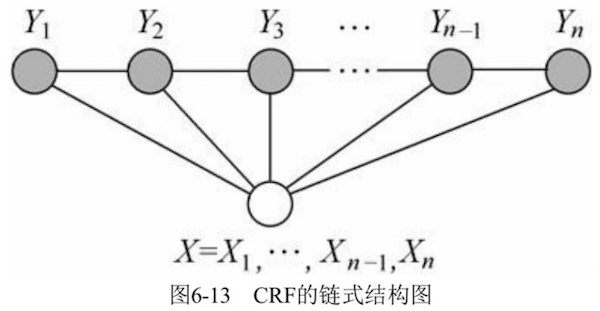
马尔可夫性质举例来说 $P(Y_2\vert X,Y_1,Y_3,\cdots,Y_n)=P(Y_2\vert X,Y_1,Y_3)$
参考MRF中团势能的定义,这里单个标注值$y_i$和观察序列$X$就构成一个极大团,团势能可以(人为)定义为:
\[\phi(y_i|X) = \exp\left(\sum_j \lambda_j t_j(y_{i-1},y_i,X,i) + \sum_k \mu_k s_k(y_i,X,i) \right)\]符号说明:
- $t_j(y_{i-1},y_i,X,i)$ 是转移函数(transition),表示对观测序列$X$的标注序列$Y$在$i$和$i-1$位置上标记的转移概率;
- $s_k(y_i,X,i)$ 是状态函数(status),表示对观测序列$X$的标注序列$Y$在$i$位置的标记概率;
- $\lambda_j$ 和 $\mu_k$ 分别是函数 $t_j$ 和 $s_k$ 的权重,需要从训练样本中估计。
对整个CRF建模:
\[\begin{align} P(Y|X) &= \frac1Z \prod_i \phi(y_i|X) \\ &= \frac1Z \prod_i \exp\left(\sum_i \sum_j \lambda_j t_j(y_{i-1},y_i,X,i) + \sum_i \sum_k \mu_k s_k(y_i,X,i) \right) \end{align}\]其中,$Z$ 还是规范化因子,保证整个函数作为概率归一化到$(0,1)$之间。
参考最大熵模型,转移函数$t$和状态函数$s$都是(人为)定义出来的特征函数。
总之,CRF建模过程大概就是这样,这样捋一下可能看书更容易理解了。如果要实际使用可以参考CRF++。
参考
- 《统计自然语言处理》宗成庆
- Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data, J Lafferty, 2001
- An Introduction to Conditional Random Fields, Charles Sutton, 2010 (照理说CRF只看这篇论文就够了,不过很长,90页……)