我们了解到通过SVD可以进行LSA,把给定文档投影到语义空间,但语义的权重不好解释。pLSA是从概率分布的角度建模的一种方法,它假设在词和文档之间有一层主题隐语义,而主题符合多项分布,一个主题中的词项也符合多项分布,由这两层分布的模型,生成各种文档。
想象某个人要写 $N$ 篇文档,他需要确定每篇文档里每个位置上的词。假定他一共有 $K$ 个可选的主题,有 $V$ 个可选的词项,所以,他制作了 $K$ 个 $V$ 面的 “主题-词项” 骰子,每个骰子对应一个主题,骰子每一面对应要选择的词项。然后,每写一篇文档会再制作一颗 $K$ 面的 ”文档-主题“ 骰子;每写一个词,先扔该骰子选择主题;得到主题的结果后,使用和主题结果对应的那颗”主题-词项“骰子,扔该骰子选择要写的词。他不停的重复如上两个扔骰子步骤,最终完成了这篇文档。重复该方法 $N$ 次,则写完所有的文档。在这个过程中,我们并未关注词和词之间的出现顺序,所以pLSA也是一种词袋方法;并且我们使用两层概率分布对整个样本空间建模,所以pLSA也是一种混合模型。
具体来说,该模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别 $z_k \in \brace{z_1,\dots,z_K}$ 。有如下三个相关的概率: $P(d_i)$ 表示词在文档 $d_i$ 中出现的概率, $P(w_j\vert z_k)$ 表示某个词 $w_j$ 在给定主题 $z_k$ 下出现的概率, $P(z_k\vert d_i)$ 表示某个主题 $z_k$ 在给定文档 $d_i$ 下出现的概率。利用这三个概率,我们可以按照如下方式得到“词-文档”的生成模型:
- 按照概率 $P(d_i)$ 选择一篇文档 $d_i$
- 按照概率 $P(z_k\vert d_i)$ 选择一个隐含的主题类别 $z_k$
- 按照概率 $P(w_j\vert z_k)$ 生成一个词 $w_j$
这样可以得到文档中每个词的生成概率。把这个过程用数学方法表示:
\[\begin{align} P(d_i,w_j) &= P(d_i)P(w_j|d_i) \\ &= P(d_i) \sum_{k=1}^K P(w_j|z_k)P(z_k|d_i) \end{align}\]用概率图表示如下:
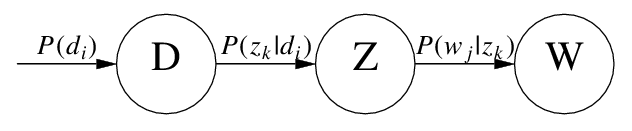
Hofmann的原始论文里使用概率符号 $P(w_j\vert z_k)$ 和 $P(z_k\vert d_i)$ ,我们也可以从矩阵的角度来描述这两个变量:
假设用 $\phi_k$ 表示词表 $\mathcal{V}$ 在主题 $z_k$ 上的一个多项分布,则 $\phi_k$ 可以表示成一个向量,每个元素 $\phi_{k,j}$ 表示词项 $w_j$ 出现在主题 $z_k$ 中的概率,即
\[P(w_j|z_k) = \phi_{k,j}, \quad \sum_{w_j \in \mathcal{V}} \phi_{k,j} = 1\]同样,假设用 $\theta_i$ 表示所有主题 $\mathcal{Z}$ 在文档 $d_i$ 上的一个多项分布,则 $\theta_i$ 可以表示成一个向量,每个元素 $\theta_{i,k}$ 表示主题 $z_k$ 出现在文档 $d_i$ 中的概率,即
\[P(z_k|d_i) = \theta_{i,k}, \quad \sum_{z_k \in \mathcal{Z}} \theta_{i,k} = 1\]最终我们要求解的参数是这两个矩阵:
\[\begin{align} \Phi &= [\phi_1,\cdots,\phi_K], \quad z_k \in \mathcal{Z} \\ \Theta &= [\theta_i, \cdots, \theta_N], \quad d_i \in \mathcal{D} \end{align}\]由于词和词之间是互相独立的,于是可以得到整篇文档的词的分布;并且文档和文档也是互相独立的,于是我们可以得到整个样本的词的分布:
\[\begin{align} P(\mathcal{W}|d_i) &= \prod_{j=1}^M P(d_i, w_j)^{n(d_i,w_j)} \\ P(\mathcal{W}|\mathcal{D}) &= \prod_{i=1}^N \prod_{j=1}^M P(d_i, w_j)^{n(d_i,w_j)} \end{align}\]其中, $n(d_i,w_j)$ 表示词项 $w_j$ 在文档 $d_i$ 中的词频, $n(d_i)$ 表示文档 $d_i$ 中词的总数,显然有 $n(d_i) = \sum_{w_j \in \mathcal{V}} n(d_i, w_j)$ 。
于是,可以很容易写出样本分布的对数似然函数:
\[\begin{align} \ell(\Phi, \Theta) &= \sum_{i=1}^N \sum_{j=1}^M n(d_i, w_j) \log P(d_i, w_j) \\ &= \sum_{i=1}^N n(d_i) \left(\log P(d_i) + \sum_{j=1}^M {n(d_i,w_j) \over n(d_i)} \log\sum_{k=1}^K P(w_j|z_k)P(z_k|d_i)\right) \\ &= \sum_{i=1}^N n(d_i) \left(\log P(d_i) + \sum_{j=1}^M {n(d_i,w_j) \over n(d_i)} \log\sum_{k=1}^K \phi_{k,j} \theta_{i,k} \right) \end{align}\]我们需要最大化对数似然函数来求解参数,对于这种含有隐变量的最大似然估计,我们还是需要使用EM方法。
E-step: 假定参数已知,计算此时隐变量的后验概率。
利用贝叶斯法则,可以得到:
\[\begin{align} P(z_k|d_i,w_j) &= {P(z_k, d_i, w_j) \over \sum_{l=1}^K P(z_l, d_i, w_j)} \\ &= {P(w_j|d_i, z_k)P(z_k|d_i)P(d_i) \over \sum_{l=1}^K \left( P(w_j|d_i,z_l)P(z_l|d_i)P(d_i) \right)} \\ &= {P(w_j|z_k)P(z_k|d_i) \over \sum_{l=1}^K P(w_j|z_l)P(z_l|d_i)} \\ &= {\phi_{k,j} \theta_{i,k} \over \sum_{l=1}^K \phi_{l,j} \theta_{i,l} } \end{align}\]这需要一点贝叶斯网络和概率图模型的知识,具体可以参考PRML第八章。
M-step:带入隐变量的后验概率,最大化样本分布的对数似然函数,求解相应的参数。
观察上面的对数似然函数 $\ell$ ,由于 $P(d_i) \propto n(d_i)$ 也就是文档长度可以单独从样本计算,可以去掉不影响最大化似然函数;此外,根据E-step的计算结果,把 $\phi_{k,j} \theta_{i,k} = P(z_k\vert d_i,w_j) \sum_{l=1}^K \phi_{l,j} \theta_{i,l}$ 代入 $\ell$ ,于是我们最大化下面这个函数即可:
\[\ell = \sum_{i=1}^N \sum_{j=1}^M n(d_i, w_j) \sum_{k=1}^K P(z_k|d_i,w_j) \log \left[ \phi_{k,j} \theta_{i,k} \right]\]这是一个多元函数求极值问题,并且已知有如下约束条件:
\[\sum_{j=1}^M \phi_{k,j} = 1 \\ \sum_{k=1}^K \theta_{i,k} = 1\]一般处理这种带有约束条件的极值问题,我们常用的方法是拉格朗日乘数法,引入拉格朗日乘子把约束条件和多元函数结合在一起,转化为无条件极值问题。这里我们引入两个乘子 $\tau$ 和 $\rho$ ,可以写出拉格朗日函数,如下:
\[\mathcal{H} = \mathcal{L}^c + \sum_{k=1}^K \tau_k \left(1- \sum_{j=1}^M \phi_{k,j}\right) + \sum_{i=1}^N \rho_i \left(1- \sum_{k=1}^K \theta_{i,k}\right)\]需要求解 $\phi_{k,j}$ 和 $\theta_{i,k}$ ,分别求偏导,取0,可得如下等式:
\[\sum_{i=1}^N n(d_i, w_j)P(z_k|d_i,w_j) - \tau_k \phi_{k,j}=0, \quad 1 \leq j \leq M, 1 \leq k \leq K \\ \sum_{j=1}^M n(d_i, w_j)P(z_k|d_i,w_j) - \rho_i \theta_{i, k}=0, \quad 1 \leq i \leq N, 1 \leq k \leq K\]消去拉格朗日乘子,最终可估计出参数:
\[\begin{align} \phi_{k,j} &= {\sum_{i=1}^N n(d_i,w_j)P(z_k|d_i,w_j) \over \sum_{m=1}^M\sum_{i=1}^N n(d_i,w_m)P(z_k|d_i,w_m)} \\ \theta_{i, k} &= {\sum_{j=1}^M n(d_i,w_j)P(z_k|d_i,w_j) \over n(d_i)} \end{align}\]参考
- Thomas Hofmann, Unsupervised Learning by Probabilistic Latent Semantic Analysis, Machine Learning, 42, 177–196, 2001
- Qiaozhu Mei, ChengXiang Zhai, A Note on EM Algorithm for Probabilistic Latent Semantic Analysis (从混合模型的角度推导pLSA)
- Liangjie Hong, Probabilistic Latent Semantic Analysis (从两层多项分布出发逐步推导,理解了Hofmann的论文再去阅读更有裨益)