随机采样算法

Posted on |

[TOC]

\[\newcommand{\x}{\boldsymbol{x}} \newcommand{\y}{\boldsymbol{y}}\]

统计学中，有时我们需要获得某一个分布的样本， 比如我们想获得 [0,1] 之间几个均匀随机数， 就可以说对 [0,1] 之间的均匀分布进行采样。

对于特定的分布， 有的我们可以从获得服从这个分布的样本， 比如一条街上每天交通事故的数量服从泊松分布， 我们把每天的数据收集起来，就可以得到服从这个分布的样本集。但有时直接采样有困难， 或者成本太高。所以，我们想办法用计算机来模拟采样。

独立样本

参考：http://bindog.github.io/blog/2015/05/20/different-method-to-generate-normal-distribution/

拒绝采样（Rejection sampling）

http://blog.csdn.net/bemachine/article/details/12584971

【注意】需要已知目标分布pdf。

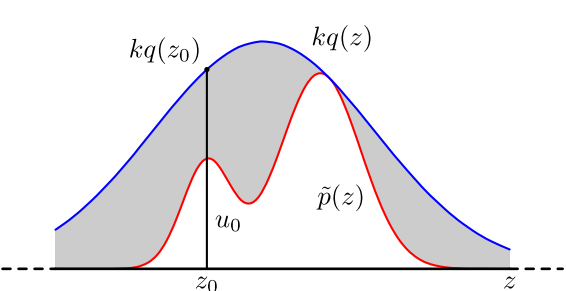
使用场景是有些函数$p(x)$太复杂在程序中没法直接采样，那么可以设定一个程序可抽样的分布$q(x)$比如正态分布等等，然后按照一定的方法拒绝某些样本，达到接近$p(x)$分布的目的： rejection sampling

具体操作如下，设定一个方便抽样的函数$q(x)$，以及一个常量$k$，使得$p(x)$总在$kq(x)$的下方。

  • $x$轴方向：从$q(x)$分布抽样得到$a$
  • $y$轴方向：从均匀分布$(0,kq(a))$中抽样得到$u$
  • 如果刚好落到灰色区域：$u>p(a)$，拒绝；否则接受这次抽样
  • 重复以上过程

Acceptance-Rejection Method

不过在高维的情况下，拒绝采样会出现两个问题，第一是合适的$q$分布比较难以找到，第二是很难确定一个合理的$k$值。这两个问题会造成图中灰色区域的面积变大，从而导致拒绝率很高，无用计算增加。

反变换法（Inverse CDF）

【注意】需要已知目标分布cdf。

假设$u=F(x)$是一个概率分布函数(CDF)，$F^{-1}$是它的反函数，若$U\sim \text{uniform}(0,1)$，则$F^{-1}(U)$服从函数$F$给出的分布。

例如，要生成一个服从指数分布的随机变量，我们知道指数分布CDF为$F(x)=1−e^{-\lambda x}$，其反函数为 $F^{ - 1}(x) = -\frac{\ln (1-x)}{\lambda}$ 。程序实现：

import matplotlib.pyplot as plt
import numpy as np

def getExponential(SampleSize,p_lambda):
    result = -np.log(1-np.random.uniform(0,1,SampleSize))/p_lambda
    return result

# 生成10000个数，观察它们的分布情况
SampleSize = 10000
es = getExponential(SampleSize, 1)
plt.hist(es,np.linspace(0,5,50),facecolor="green")
plt.show()

那么为什么$F^{-1}(U)$会服从$F$给出的分布呢？

证明：$P(F^{-1}(U)\le x)$，两边同时取$F$得到$P(F^{−1}(U)\le x)=P(U\le F(x))$，根据均匀分布的定义$P(U<y)=y$，所以$P(U\le F(x))=F(x)$，即$P(F^{−1}(U)\le x)=F(x)$，刚好是随机变量服从某个分布的定义，证毕。

\[\begin{align} P(F^{-1}(U) \le x) & =P(U \le F(x)) \\ & = F(x) \end{align}\]

相关样本

参考：

  • https://cos.name/2013/01/lda-math-mcmc-and-gibbs-sampling/
  • https://applenob.github.io/1_MCMC.html
  • http://www.cnblogs.com/daniel-D/p/3388724.html （附带python实现）

解决rejection sampling在高维空间碰到的问题。

Markov Chain

符号：

  • 时刻$t$随机变量$X_t$
  • 状态$i$、$j$
  • 从状态$i$到状态$j$的转移概率$P_{ij}$

Markov链体现的是状态空间的转换关系，下一个状态只取决于当前的状态。

Markov链
考虑只取有限个值的随机过程 ${X_t,t=0,1,2\cdots}$，若$X_t=i$，即在时刻$t$处于状态$i$，则下一时刻$t+1$将处于状态$j$的概率是固定的$P_{ij}$，即对一切状态有
\[P(X_{t+1}=j|X_t=i,X_{t-1}=i_{t-1},\cdots,X_1=i_1,X_0=i_0) = P_{ij}\]
收敛定理
如果一个非周期Markov链具有转移概率矩阵$P$，且它的任何两个状态是连通的，那么$\displaystyle \lim_{n\to \infty}P_{ij}^n$存在且与之前状态$i$无关，记$\displaystyle \lim_{n\to \infty} P_{ij}^n=\pi(j)$。

我们有

\[\displaystyle \lim_{n \rightarrow \infty} P^n =\begin{bmatrix} \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \pi(1) & \pi(2) & \cdots & \pi(j) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}\]

其中，矩阵每一行

\[\pi = [\pi(1), \pi(2), \cdots, \pi(j),\cdots ], \quad \sum_{i=0}^{\infty} \pi(i) = 1\]

$\pi$称为Markov链的平稳分布。其中，$\pi(i)$表示状态$i$的概率分布。

细致平稳条件（Detailed Balance Condition）
对于任何两个状态$i,j$ 从 $i$ 转移出去到$j$ 而丢失的概率质量，恰好会被从 $j$ 转移回 $j$ 的概率质量补充回来，此时$\pi$达到平稳分布。
\[\pi(i)P_{ij} = \pi(j)P_{ji} \quad\quad \text{for all} \quad i,j \tag{1}\]

从初始时刻$0$的概率分布$\pi_0$出发，进行Markov随机过程（状态转移），记时刻$n$的$X_n$的概率分布为$\pi_n$，则有

\[\begin{aligned} X_0 &\sim \pi_0 \\ X_n &\sim \pi_n, \qquad \pi_n=\pi_{n-1}P=\pi_0 P^n \end{aligned}\]

由Markov链收敛定理，概率分布$\pi_n$将收敛到平稳分布$\pi$，有

\[\begin{aligned} X_0 & \sim \pi_0 \\ X_1 & \sim \pi_1 \\ & \cdots \\ X_n & \sim \pi_n=\pi \\ X_{n+1} & \sim \pi \\ X_{n+2}& \sim \pi \\ & \cdots \end{aligned}\]

所以，$X_n,X_{n+1},X_{n+2},\cdots \sim \pi$ 都是同分布的随机变量，当然他们并不独立。即对这些变量采样得到的状态$k$服从分布$\pi$。

MCMC

【注】需要已知pdf，该pdf的积分难求。

对给定概率分布$p(x)$，如果能够构造一个转移矩阵$P$，使得该Markov链的平稳分布恰好是$p(x)$，那么就能在Markov链收敛后获得服从该分布的样本了。

改变一下符号：

  • 用$p(i)$替代$\pi(i)$表示状态$i$的概率分布
  • 用$q(i,j)$替代$P_{ij}$表示状态$i$到$j$的转移概率，也可以写作$q(j\vert i)$或$q(i->j)$

显然，通常情况下，细致平稳条件不成立， \(p(i) q(i,j) \neq p(j) q(j,i)\)

引入$\alpha(i,j)= p(j) q(j,i)$，$\alpha(j,i) = p(i) q(i,j)$，使得细致平稳条件成立：

\[p(i) \underbrace{q(i,j)\alpha(i,j)}_{Q'(i,j)} = p(j) \underbrace{q(j,i)\alpha(j,i)}_{Q'(j,i)} \tag{2}\]

于是我们把原来具有转移矩阵 $Q$ 的一个普通Markov链，改造为了具有转移矩阵$Q′$的Markov链，而 $Q′$ 恰好满足细致平稳条件，由此Markov链 $Q’$ 的平稳分布就是 $p(x)$。

引入的 $\alpha(i,j)$ 称为接受率，物理意义可以理解为在原来的Markov链上，从状态 $i$ 以 $q(i,j)$ 的概率转跳转到状态 $j$ 的时候，我们以 $\alpha(i,j)$ 的概率接受这个转移，于是得到新的Markov链 $Q′$ 的转移概率为 $q(i,j)\alpha(i,j)$。

【MCMC采样算法】

  1. 初始化Markov链初始状态 $X_0=x_0$
  2. 对时刻 $t=0,1,2,\cdots$，循环以下过程采样：
    • 第$t$时刻Markov链状态为$X_t=x_t$，采样新状态$y\sim q(x\vert x_t)$
    • 从均匀分布采样$u\sim \text{Uniform}(0, 1)$
    • 如果$u\lt \alpha(x_t,y) = p(y)q(x_t\vert y)$，则接受转移$x_t\to y$，即$X_{t+1}=y$
    • 否则，不接受转移，即$X_{t+1}=x_t$

Metropolis-Hasting算法

默认MCMC算法里，接受率$\alpha$值偏小，会导致拒绝率过高。可以把细致平稳条件$(2)$式中的$\alpha(i,j)$和$\alpha(j,i)$同比例放大，既不会破坏细致平稳条件，而且可以提高跳转中的接受率，从而得到Metropolis-Hastings算法。

\[\alpha(i,j) = \min\left\{\frac{p(j)q(j,i)}{p(i)q(i,j)},1\right\}\]

【Metropolis-Hastings算法】

  1. 初始化Markov链初始状态 $X_0=x_0$
  2. 对时刻 $t=0,1,2,\cdots$，循环以下过程采样：
    • 第$t$时刻Markov链状态为$X_t=x_t$，采样新状态$y\sim q(x\vert x_t)$
    • 从均匀分布采样$u\sim \text{Uniform}(0, 1)$
    • 如果$u\lt \alpha(x_t,y) = \min\left{\frac{p(y)q(x_t\vert y)}{p(x_t)q(y\vert x_t)},1\right}$，则接受转移$x_t\to y$，即$X_{t+1}=y$
    • 否则，不接受转移，即$X_{t+1}=x_t$

以上算法里的$x$不要求是一维的，对高维空间$p(\x)$，如果满足细致平稳条件

\[P(\x)Q'(\x\to\y) = p(\y)Q'(\y\to\x)\]

那么以上M-H算法同样有效。

参考代码：

  • https://github.com/tback/MLBook_source/blob/master/14%20MCMC/MH.py
  • https://gist.github.com/qxj/66d42234f58d519b2511ed2892cf7411

Gibbs sampling

对于高维的情形，由于接受率 $\alpha$ 的存在(通常 $\alpha\lt 1$), 以上 Metropolis-Hastings 算法的效率仍然不够高。能否找到一个转移矩阵$Q$使得接受率 $\alpha=1$ 呢？

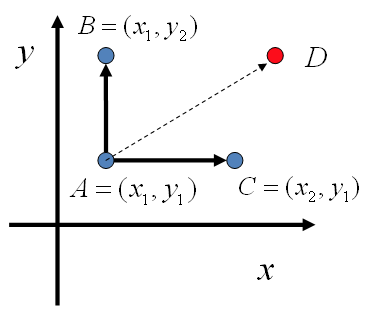
Gibbs sampling

假设两个随机变量$x$和$y$，在$x=x_1$这条平行于 $y$ 轴的直线上，如果使用条件分布 $p(y\vert x_1)$ 做为任何两个点之间的转移概率，那么任何两个点之间的转移满足细致平稳条件。同样的，如果我们在 $y=y_1$ 这条直线上任意取两个点 $A(x_1,y_1),C(x_2,y_1)$，也一样。

\[p(A)p(y_2\vert x_1) = p(B)p(y_1\vert x_1) \\ p(A)p(x_2\vert y_1) = p(C)p(x_1\vert y_1)\]

于是，可以构造出平面上任意两点之间的转移概率矩阵$Q$：

\[\begin{align*} Q(A\to B) & = p(y_B|x_1) & \text{if} \quad x_A=x_B=x_1 & \\ Q(A\to C) & = p(x_C|y_1) & \text{if} \quad y_A=y_C=y_1 & \\ Q(A\to D) & = 0 & \text{otherwise.} & \end{align*}\]

有了如上的转移矩阵 $Q$, 我们很容易验证对平面上任意两点 $X,Y$, 满足细致平稳条件

\[p(X)Q(X\to Y) = p(Y) Q(Y\to X)\]

于是这个二维空间上的Markov链将收敛到平稳分布 $p(x,y)$。而这个算法就称为 Gibbs Sampling 算法。

【n维Gibbs Sampling算法】

  1. 随机初始化${x_i: i=1,\cdots,n}$
  2. 对时刻$t=0,1,2,\cdots$ 按各维度循环采样
    • $x_1^{(t+1)}\sim p(x_1\vert x_2^{(t)},x_3^{(t)},\cdots,x_n^{(t)})$
    • $x_2^{(t+1)}\sim p(x_2\vert x_1^{(t+1)},x_3^{(t)},\cdots,x_n^{(t)})$
    • $\cdots$
    • $x_j^{(t+1)}\sim p(x_j\vert x_1^{(t+1)},\cdots,x_{j-1}^{(t+1)},x_{j+1}^{(t)},\cdots,x_n^{(t)})$
    • $\cdots$
    • $x_n^{(t+1)}\sim p(x_1\vert x_n^{(t+1)},x_2^{(t+1)},\cdots,x_{n-1}^{(t+1)}) $

参考代码：

  • https://github.com/tback/MLBook_source/blob/master/14%20MCMC/Gibbs.py