[TOC]
\[\newcommand{\T}{\mathsf{T}} \newcommand{\X}{\boldsymbol{X}} \newcommand{\x}{\boldsymbol{x}} \newcommand{\y}{\boldsymbol{y}} \newcommand{\W}{\boldsymbol{\theta}} \newcommand{\tr}{\mathrm{tr}}\]Batch GD、mini-batch GD、SGD、online GD的区别在于更新一次参数所用到训练数据:
| / | batch | mini-batch | Stochastic | Online |
|---|---|---|---|---|
| 训练集 | 固定 | 固定 | 固定 | 实时更新 |
| 单次迭代样本数 | 整个训练集 | 训练集的子集 | 单个样本 | 根据具体算法定 |
| 算法复杂度 | 高 | 一般 | 低 | 低 |
| 时效性 | 低 | 一般(delta 模型) | 一般(delta 模型) | 高 |
| 收敛性 | 稳定 | 较稳定 | 不稳定 | 不稳定 |
Batch GD
每次迭代的梯度方向计算由所有训练样本共同投票决定。
假设参数 $\theta$ 有 $n$ 维,对L2损失求解第 $j$ 维的一阶偏导数:
\[{\partial L(\theta) \over \partial \theta_j} = \frac{1}{m} \sum_{i=1}^m \left(y^{(i)} - h_\theta(x^{(i)})\right) x_j^{(i)}+ \lambda \theta_j\]【注】这里的梯度就是迭代的下降方向。不同优化方法其实主要区别就是这个方向不同,SGD是求解损失函数的一阶导数(梯度,Gradient),牛顿法是二阶导数(海森矩阵,Hessian Matrix)。
训练算法为:
\[\begin{array}{l} \text{repeat until convergency } \{ \\ \quad \text{for j=1; j<n; j++ :} \\ \qquad \theta_j : = \theta_j - \alpha \left( \frac{1}{m}\sum_{i = 1}^m \left( y^{(i)} - h_\theta(x^{(i)}) \right) x_j^{(i)}+ \lambda \theta_j \right) \\ \} \end{array}\]batch GD算法是计算损失函数在整个训练集上的梯度方向,沿着该方向搜寻下一个迭代点。batch的含义是每轮迭代会根据所有样本算出梯度,再更新模型,然后才进入下一轮在新模型的基础上继续迭代。
【注】squared loss和log loss推导出的梯度形式是一样的,主体都是 $ \left( y^{(i)} - h_\theta(x^{(i)}) \right) x_j^{(i)}$。
http://spark.apache.org/docs/latest/mllib-linear-methods.html#loss-functions
Stochastic GD
随机梯度下降(SGD)就是每次从所有训练样例中抽取一个样本计算梯度并立刻更新模型,这样每次更新模型并不用遍历所有数据集,迭代速度会很快;但是会增加很多迭代次数,因为每次选取的方向不一定是全局最优的方向。
\[\begin{array}{l} \text{repeat until convergency } \{ \\ \quad \text{random choice sample }i\text{ from whole }m\text{ training samples:} \\ \quad \text{for j=1; j<n; j++ :} \\ \qquad \theta_j : = \theta_j - \alpha \left( \left( y^{(i)} - h_\theta(x^{(i)}) \right) x_j^{(i)} + \lambda \theta_j \right) \\ \} \end{array}\]Mini-batch GD
这是介于以上两种方法的折中,每次随机选取大小为b的mini-batch(b<m),算完之后再更新模型,这样既节省了计算整个批量的时间,同时基于mini-batch计算的方向对比单个样本来说也会更加准确。
\[\begin{array}{l} \text{repeat until convergency } \{ \\ \quad \text{random choice }b\text{ samples from whole }m\text{ training samples:} \\ \quad \text{for j=1; j<n; j++ :} \\ \qquad \theta_j : = \theta_j - \alpha \left( \frac{1}{b}\sum_i^{i+b} \left( y^{(i)} - h_\theta(x^{(i)}) \right) x_j^{(i)} + \lambda \theta_j \right) \\ \} \end{array}\]可以看到,SGD等价于b=1的mini-batch GD,即每个mini-batch中只有一个训练样本。
Parallel SGD

参考:Parallelized Stochastic Gradient Descent
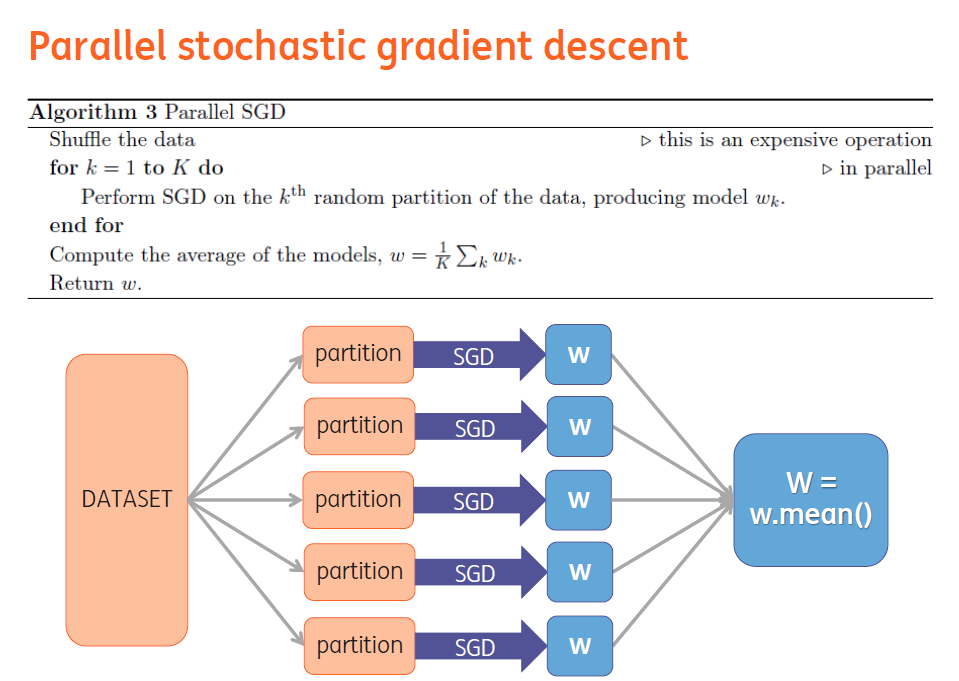
https://github.com/blebreton/spark-FM-parallelSGD
Proximal Gradient Descent
Proximity GD 用来解决 L1 正则中 0 点不可导的问题。
对于目标函数中包含加性的非平滑项并使用SGD求解的问题,可以使用proximal operator求解:
假设目标函数为 $\min_\theta f(\theta)+h(\theta)$,其中 $f(\theta)$可导,而 $h(\theta)$不可导。
\[prox(f,h) = \arg\min_\theta\{\|x-\theta\|^2_2 + \lambda\|\theta\|_1 \}\]利用subgradient可以推导得
\[prox(f,h)_i = \theta_i^* = \left\{ \begin{array}{lr} 0 & \text{if } |\theta_i| \leq \lambda \\ \theta_i - \lambda sign(\theta_i) & \text{if } |\theta_i| > \lambda \end{array}\right.\]也可以简写作
\[prox(f,h)_i = sign(\theta_i)\max(|\theta_i|-\lambda, 0)\]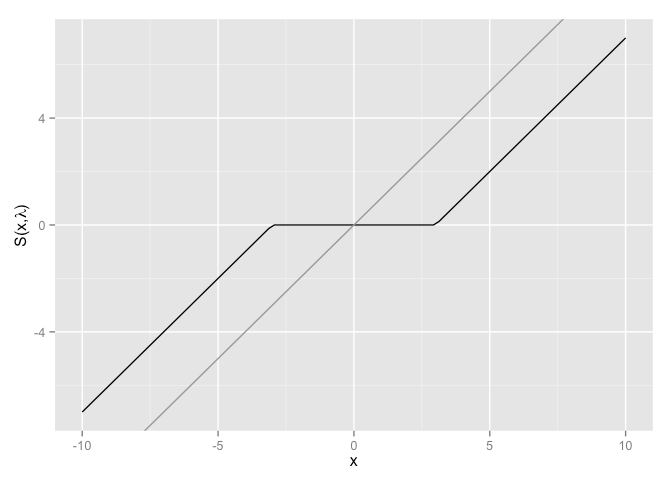
可以发现soft-thresholding方法,把$[-\lambda,\lambda]$内的参数直接置为0,而把之外的参数压缩了$\lambda$大小。
参考
- CS229第一章
- 论文:Proximal Algorithms, Boyd
- https://www.zhihu.com/question/38426074/answer/76683857
- http://breezedeus.github.io/2013/11/16/breezedeus-proximal-gd.html
- https://math.stackexchange.com/a/511106/440346
- http://jocelynchi.com/soft-thresholding-operator-and-the-lasso-solution
- 近端梯度下降 Proximal Method