文本分类技术基础

[TOC]

问题定义

分类：给定一个对象，从一个事先定义好的分类体系中挑出一个或多个最适合该对象的类别。

文本分类(Text Categorization)：在给定的分类体系下，根据文本内容自动的确定文本关联的类别。从数学角度看，文本分类是一个映射的过程，它将未标明类别的文本映射到已有的类别中，该映射可以是一对一或一对多的映射。

\[f: A \to B\]

其中， $A$ 表示待分类的文本集合， $B$ 表示分类体系中的类别集合。

文本分类属于有监督的学习(Supervised Learning)，也是NLP的一个子领域，基本步骤如下：

定义分类体系，即确定具体要分类的类别。
将预先分类过的文档作为训练集，对文档做分词、去停用词(stop words)、去无用词性、去单字词等准备工作，对英文等语言还需要做词干提取(stemming)。
确定表达模型，对文档矩阵进行降维，提取训练集中最有用的特征。
应用具体的分类模型和算法，训练出文本分类器。
在测试集上测试并评价分类器的性能。
应用性能最高的分类模型对待分类文档进行分类。

评价指标

混淆矩阵是监督学习中的一种可视化工具，主要用于比较分类结果和实例的真实信息（outcome vs. ground truth）。

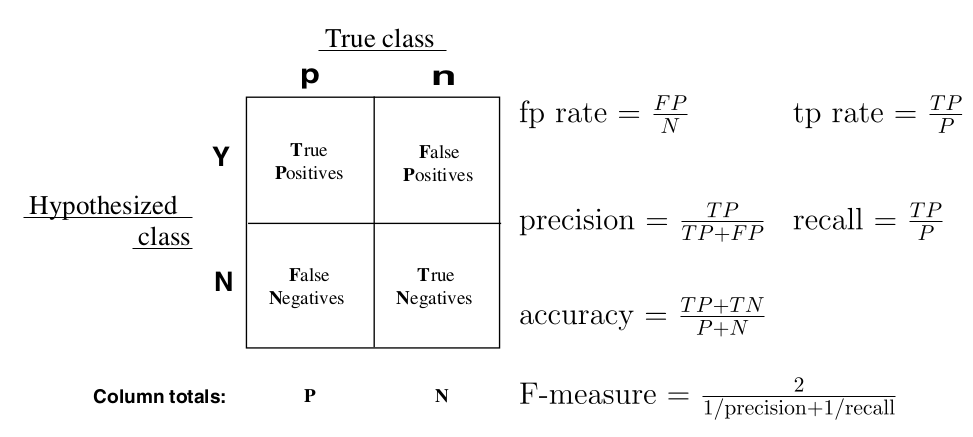
矩阵中的每一行代表实例的预测类别，每一列代表实例的真实类别。

Positive 正例
Negative 负例
True 预估为正
False 预估为负

在混淆矩阵中，每一个实例可以划分为四种类型之一：True Positive、False Positive、False Negative、True Negetive（TP/FP/FN/TN）。

由混淆矩阵可以计算一系列的评价指标，如accuracy、precision、recall等等。

准确率(P, Precision)=TP/(TP+FP)，在所有被判断为正确的文档中，有多大比例是确实正确的。
召回率(R, Recall)=TP/(TP+FN)，在所有确实正确的文档中，有多大比例被我们判为正确。
F1测度(F-measure)=2/(1/P+1/R)，是准确率和召回率的调和均值，既衡量准确率，也衡量召回率。
精确率(Accurarcy)=(TP+TN)/(P+N)，如果是多分类问题，Accuracy关注所有类别上的分类正确性，而Precision只关注单个类别上的分类正确性。

模型选择

如果要在多个模型之间选择最佳模型，常用的办法是交叉验证(cross validation)。

常用的交叉验证方法是S-fold交叉验证：

随机的把数据集切分成S个互不相交且大小相同的子集；
利用S-1个子集的数据训练模型，用剩下的那个子集测试模型；
将这一过程对可能的S种选择重复进行；
最后，选出S次评测中平均测试误差最小的模型。

特征选择

模型对每篇文档默认构造的向量是固定长度n，该n可能是我们汉语词典收录的词条数目，显然这会导致每个向量里的大部分特征值都是0。这是文本分类的主要特点：高维和 数据稀疏。所以，降维是开始运用分类算法训练样本之前的一个关键预处理步骤。

降维有两种方法：

特征选择(feature selection)，它是对原始特征利用一些评估函数独立评估，按照评估结果高低排序，选择那些评估值较高的特征。常用的特征选择方法有词频信息、互信息、信息增益和卡方检验等。
特征抽取(feature detection)，它是把原始特征映射到低维空间，这些被称为二次特征 (比如，奇异值分解后得到的lsi)，从而生成模型产生的新特征。特征抽取方法比较常用的是lsa、plsa和lda等。

【注意】特征选择和特征权重值计算是不同的，前者是根据特征对分类的重要程度来实现降维的手段，而后者是用于区分向量，实现分类算法中的相似度判断。它们是两个阶段的不同处理方法。特征权重值最典型的是tf-idf。

针对英文纯文本的实验结果表明：作为特征选择方法时，卡方检验和信息增益的效果最佳（相同的分类算法，使用不同的特征选择算法来得到比较结果）；文档频率方法的性能同前两者大体相当，术语强度方法性能一般；互信息方法的性能最差。¹

卡方检验

卡方检验(the χ² test, chi-square test)是通过计算每个特征和每个类别的关联程度，然后选择那些关联程度高的特征来实现降维。其基本思想就是衡量实际值与理论值的偏差来确定理论的正确与否。 $\chi^2$ 统计量的表达式为：

\[\chi^2 = \sum_{i=1}^n \frac{(x_i - E(x))^2}{E(x)}\]

其中， $x_i$ 是观察值， $E(x)$ 是期望值。一般用于特征选择的卡方检验方法如下：

\[\begin{align} \chi^2(t,c) &= \frac{N \times (A \times D-B \times C)^2}{(A+C) \times (B+D) \times (A+B) \times (C+D)} \\ &= \frac{(AD-BC)^2}{(A+B)(C+D)} \end{align}\]

其中， $t$ 是具体的每个特征(比如词)， $c$ 是类别号。其他各值的含义如下：

特征t	属于分类c	不属于分类c	总计
包含特征t	A	B	A+B
不包含特征t	C	D	C+D
总计	A+C	B+D	N

此外，在计算卡方检验值 $\chi^2$ 之前，除了正常的去停用词等步骤外，建议还要去低频词。比如，把一个类里出现次数小于3的词去掉。因为卡方检验存在所谓的 低频词缺陷，即低频词可能会有很高的卡方值。

因为在计算 $A$ 、 $B$ 的时候，它统计文档中是否出现词 $t$ ，却不管 $t$ 在该文档中出现了几次，这会使得他对低频词有所偏袒（因为它夸大了低频词的作用）。甚至会出现这种情况：一个词在一类文章的每篇文档中都只出现了1次，另一个词在该类文章99%的文档中出现了10次，前者的卡方值却大过了后者；其实后面的词才是更具代表性的，但只因为它出现的文档数比前面的词少了1%，特征选择的时候就可能筛掉后面的词而保留了前者。¶

最后，计算得到每个特征对应每种分类的卡方值之后，将特征按对于所有分类的卡方值之和从大到小排序，取前 $k$ 个特征即为选择的特征。

信息增益法

信息增益(information gain)是通过计算每个特征对分类贡献的信息量，贡献越大信息增益越大，然后可以选择那些信息增益较高的特征实现降维。

信息熵定义：

\[H(C) = -\sum_{i=1}^m P(c_i) \log P(c_i)\]

其中， $c_i$ 是类别变量 $C$ 可能的取值， $P(c_i)$ 是各个类别出现的概率。

条件熵定义：

\[\begin{align} H(C|T) &= \sum_{t \in T} P(t)H(C|T=t) \\ &= P(t)H(C|t) + P(\bar{t})H(C|\bar{t}) \\ &= - P(t) \sum_{i=1}^n P(C_i|t) \log P(C_i|t) - P(\bar{t})\sum_{i=1}^n P(C_i|\bar{t}) \log P(C_i|\bar{t}) \end{align}\]

其中，带 $\bar{t}$ 的值表示特征 $t$ 不出现的情况。

特征 $t$ 给系统带来的信息增益是系统原本的熵与固定特征 $T$ 后的条件熵之差。

\[g(t,c) = H(C) - H(C|T)\]

信息增益也是考虑了特征出现和不出现两种情况，与卡方检验一样，是比较全面的，因而效果不错。但信息增益最大的问题还在于它只能考察特征对整个系统的贡献，而不能具体到某个类别上，这就使得它只适合用来做所谓“全局”的特征选择（指所有的类都使用相同的特征集合），而无法做“本地”的特征选择（每个类别有自己的特征集合，因为有的词，对这个类别很有区分度，对另一个类别则无足轻重）。

分类模型

在训练阶段，就是利用各种分类算法对转化后的文本向量估计模型。常用的分类算法有朴素贝叶斯、knn、决策树、神经网络和svm等。下边主要介绍一下比较易用的朴素贝叶斯分类器。

一些基本概念：

输入空间为n维向量的集合 $\mathcal{X} \subseteq \Re^n$ ，其中向量 $\mathrm{x} \in \mathcal{X}$ ， $\mathrm{x}=(t_1,\dots,t_n)$ ，而 $t_i$ 是文档向量 $\mathrm{x}$ 的一个特征，比如，词，或者词和权重的二元组。
输出空间为类标号集合，可以是二元分类 $\mathcal{Y} =\brace{+1, -1}$ ，或者多元分类 $\mathcal{Y}=\brace{y_1,\dots,y_m}$ 。
训练数据为一组根据未知分布 $P(x, y)$ 独立采样(i.i.d)的数据集合，由输入向量与输出类标号对组成 $D=\brace{(\mathrm{x}^{(1)},y^{(1)}),\dots,(\mathrm{x}^{(l)},y^{(l)})}$ 。

假设 (hypothesis)：计算机对训练集背后的真实模型（真实的分类规则）的猜测称为假设。可以把真实的分类规则想像为一个目标函数，我们的假设则是另一个函数，假设函数在所有的训练数据上都得出与真实函数相同（或足够接近）的结果。

监督学习方法可以分为生成方法和判别方法，所学到的模型分别成为生成模型(generative model)和判别模型(discriminative model)。

生成方法由训练数据学习联合概率分布 $P(X,Y)$ ，然后求得条件概率分布 $P(Y\vert X)$ 作为预测的模型，即生成模型：

\[P(Y|X) = \frac{P(X,Y)}{P(X)}\]

这样的方法之所以称作生成模型，是因为模型表示了给定输入 $X$ 产生输出 $Y$ 的生成关系。典型的生成模型有：朴素贝叶斯法和隐马尔科夫模型。

判别方法直接学习决策函数 $f(X)$ 或者条件概率分布 $P(Y\vert X)$ 作为预测模型，即判别模型。判别方法关心的是对给定的输入 $X$ ，应该预测什么样的输出 $Y$ 。典型的判别模型有：knn、决策树、逻辑回归、EM、SVM、各种boosting算法等等。

朴素贝叶斯

根据贝叶斯公式(Bayes theorem)，文档 $X=d$ 属于类别 $Y=c_k$ 的概率，也称作 $Y=c_k$ 的后验概率正比于该类别的先验概率和条件概率的乘积：

\[\begin{align} P(Y=c_k|X=d) &= \frac{P(Y=c_k)P(X=d|Y=c_k)}{P(X=d)} \\ &\propto P(Y=c_k)P(X=d|Y=c_k) \end{align}\]

根据 极大后验概率假设(MAP, Maximum a posteriori probability hypothesis)，使得后验概率 $P(Y=c_k\vert X=d)$ 最大的那个类别号误差最小，即得到贝叶斯分类器：

\[c_k = \operatorname*{arg\,max}_{c_k} P(Y=c_k)P(X=d|Y=c_k)\]

假定文档可以用向量表示 $d=(t_1,\dots,t_n)$ ，其中 $t_i$ 表示文档的属性值。则上式可以写成：

\[c_k = \operatorname*{arg\,max}_{c_k} P(c_k)P(t_1,\dots,t_n|c_k)\]

朴素贝叶斯分类器之所以朴素，是基于一个简单的假设：文档的词之间互相条件独立，即观察到 $t_1,\dots,t_n$ 的联合概率等于每个词的概率乘积。由于词之间相互条件独立，对每个词的参数就可以分别估计，这大大简化了计算，使它尤其适合词数量非常大的文本分类问题。

最终得到的朴素贝叶斯分类器方法如下：

\[c_k = \operatorname*{arg\,max}_{c_k} P(c_k)\prod_i P(t_i|c_k)\]

实际使用中避免乘法导致浮点数下界溢出，一般转换为对数计算，不改变凸函数性质：

\[c_k= \operatorname*{arg\,max}_{c_k} \log P(c_k) + \sum_i \log P(t_i|c_k)\]

其中， $P(t_i\vert c_k)$ 表示分类 $c_k$ 下单个词的条件概率。

参数估计

可见只要知道先验概率 $P(c_k)$ 和条件概率分布 $P(t_i\vert c_k)$ 就可以设计出一个贝叶斯分类器。事实上，几乎所有的基于统计的分类问题都是在做这样一件事情：由训练集数据来估计实际的条件概率分布。

先验概率 $P(c_k)$ 只是一个概率值，容易取其最大似然估计值：

\[P(c_k) = \frac{N(c_k)}{\sum_{i=1}^m N(c_i)}\]

其中， $N(c_i)$ 是类别 $c_i$ 的文档的总数， $m$ 是类别总数。有时候也会加入平滑因子，比如：

\[P(c_k) = \frac{N(c_k)}{\sum_{i=1}^m N(c_i)} \approx \frac{1+N(c_k)}{m + \sum_{i=1}^m N(c_i)}\]

条件概率分布 $P(t_i\vert c_k)$ 服从某种形式分布的概率密度函数，需要从训练集中样本特征的分布情况进行估计。一般的文本分类问题，常假设词的独立概率分布服从多项式分布，相应模型称作多项式模型(Multinomial model)。在多项式模型中，假定文档 $d$ 由 $l$ 个不同的词项构成，每个词出现的位置与其他词是互相独立的，其独立概率为 $P(t_i\vert c_k)$ ，每个词可以重复出现，次数即在文档 $d$ 中的词频记为 $\mathrm{df}_d(t_i)$ 。根据多项式分布的概率公式：

\[\begin{align} f(x_1,\dots,x_k;n,p_1,\dots,p_k) &= \Pr(X_1 = x_1\mbox{ and }\dots\mbox{ and }X_k = x_k) \\ & = { {n! \over x_1!\cdots x_k!} p_1^{x_1}\cdots p_k^{x_k}}, \quad \sum_{i=1}^k x_i=n \end{align}\]

其中，共有 $n$ 次试验，即每个文档中的词数； $x_i$ 是第 $i$ 项出现的次数，即某词项在该文档中的词频； $p_i$ 是第 $i$ 项出现的概率，即某词项在该类文档中出现的概率。可知文档 $d$ 属于类别 $c_k$ 的条件概率：

\[P(d|c_k) = \frac{\left(\sum_{i=1}^l \mathrm{df}_d(t_i)\right)!}{\prod_{i=1}^l \mathrm{df}_d(t_i)!} \prod_{i=1}^l P(t_i|c_k)^{\mathrm{df}_d(t_i)}\]

代入贝叶斯公式，得到

\[c_k = \operatorname*{arg\,max}_{c_k} \log P(c_k) + \sum_{i=1}^l \mathrm{df}_d(t_i) \log P(t_i|c_k)\]

其中， $\mathrm{df}_d(t_i)$ 表示词项 $t_i$ 在文档 $d$ 中的词频，也就是说多项式模型下，可以根据该文档中每个词(可重复，即等于词频)所属类别的概率来估计该文档所属类别的条件概率。

为了避免某个词属于某类别的概率为0，实际参数估计时也会加入平滑因子，常用Lapalace平滑：

\[P(t_i|c_k) = \frac{N(t_i, c_k)}{\sum_{j=1}^n N(t_j, c_k)} \approx \frac{1+N(t_i, c_k)}{n+\sum_{j=1}^n N(t_j, c_k)}\]

其中， $N(t_i, c_k)$ 表示词 $t_i$ 在类别 $c_k$ 的文档中出现的次数， $n$ 表示词的总数。

算法伪代码如下：

def train(CLASSIFIED_DOCUMENTS):
    '''CLASSIFIED_DOCUMENTS = ((d_1, c_1), ..., (d_n, c_m))
    '''
    N = len(CLASSIFIED_DOCUMENTS)
    DOC_COUNT_OF_CLASS = {}
    TERM_COUNT_OF_CLASS = {}
    TERM_MATRIX = {}
    for d, c in CLASSIFIED_DOCUMENTS:
        DOC_COUNT_OF_CLASS[c] += 1
        for t in WordSegment(d):
            TERM_COUNT_OF_CLASS[c] += 1
            TERM_MATRIX[t][c] += 1    # TODO: handle exception
    priorprob = {}
    condprob = {}
    for c_k in DOC_COUNT_OF_CLASS:
        N_c = DOC_COUNT_OF_CLASS[c_k]
        priorprob[c_k] = (1+N_c)/(len(DOC_COUNT_OF_CLASS)+N)
    for t in TERM_MATRIX:
        for c in DOC_COUNT_OF_CLASS:
            N_tc = TERM_MATRIX[t][c]  # TODO: handle exception
            condprob[t][c] = (1+N_tc)/(len(TERM_MATRIX)+TERM_COUNT_OF_CLASS[c])
    return priorprob, condprob

def classify(DOCUMENT, priorprob, condprob):
    '''DOCUMENT = d_i
    '''
    terms = WordSegment(DOCUMENT)
    max_score = -float('Inf')
    c_k = None
    for c in priorprob:
        score = log(priorprob[c])
        for t in terms:
            score += log(condprob[t][c])
        if score > max_score:
            max_score = score
            c_k = c
    return c_k

贝努利模型

另常用的一种参数估计方法是假设词的独立概率服从二项分布或贝努利分布，相应模型称作贝努利模型(Bernoulli model)。

它使用二值向量表示一个文档，即 $d=(t_1,\dots,t_n), t_i \in \brace{0,1}$ ，其中， $n$ 表示词项的总数， $t_i=1$ 表示词 $t_i$ 在文档 $d$ 中出现过，否则 $t_i=0$ 即未出现。根据二项分布的概率公式：

\[\begin{align} f(k;n,p) &= \Pr(X = k) \\ &= \binom{n}{k} p^k(1-p)^{n-k} \end{align}\]

此时， $n=1$ 且 $k \in \brace{0,1}$ 即贝努利分布，可知单个词的条件概率 $P(t_i\vert c_k)$ ：

\[\begin{align} P(t_i|c_k) &= P(t_i=1|c_k)^{t_i}\left(1-P(t_i=1|c_k)\right)^{1-t_i} \\ &= \left(\frac{P(t_i=1|c_k)}{1-P(t_i=1|c_k)}\right)^{t_i}\left(1-P(t_i=1|c_k)\right) \end{align}\]

贝努利模型假定对于给定的类别 $c_k$ ，训练集中的每个词在文档 $d$ 中是否出现相互独立，于是文档 $d$ 可以看作是 $n$ 次独立的贝努利实验， $n$ 是训练集中词的总数。把条件概率代入上面的贝叶斯公式，可得：

\[\begin{align} c_k &= \arg\max_{c_k} \log P(c_k) + \sum_{i=1}^n \log\left(1-P(t_i=1|c_k)\right) + \sum_{i=1}^n t_i \log \frac{P(t_i=1|c_k)}{1-P(t_i=1|c_k)} \\ &= \arg\max_{c_k} \log P(c_k) + \sum_{i=1}^n \log P(t_i=1|c_k) \end{align}\]

其中， $n$ 是所有词的数量。也就是说贝努利模型下，需要根据所有词出现的概率来估计条件概率。

计算单个词在某类别文档里出现的概率，加入平滑因子后估计公式为:

\[P(t_i=1|c_k) = \frac{N(t_i, c_k)}{N(c_k)} \approx \frac{1+N(t_i,c_k)}{2+N(c_k)}\]

其中， $N(t_i,c_k)$ 表示包含词 $t_i$ 且属于类别 $c_k$ 的文档数， $N(c_k)$ 表示属于类别 $c_k$ 的文档数。

贝努利模型属于二值模型，对于每个词只统计是否出现，而不计算其出现次数；不同于多项式模型，贝努利模型对未出现的词也要显式建模，即在应用分类器的时候，对文档中未出现的词的条件概率也计算到总的条件概率里。可以想象，如果总的词数很多，贝努利模型会导致文档向量很长。一般来讲，多项式模型适合处理长文本，而贝努利模型最好用来处理短文本。由于贝努利模型计算训练集中每个词的出现概率，它对噪声比较敏感，所以在使用之前必须要做特征选择。

算法伪代码如下：

def train(CLASSIFIED_DOCUMENTS):
    '''CLASSIFIED_DOCUMENTS = ((d_1, c_1), ..., (d_n, c_m))
    '''
    N = len(CLASSIFIED_DOCUMENTS)
    DOC_COUNT_OF_CLASS = {}
    TERM_MATRIX = {}
    for d, c in CLASSIFIED_DOCUMENTS:
        DOC_COUNT_OF_CLASS[c] += 1
        for t in set(WordSegment(d)):
            TERM_MATRIX[t][c] += 1
    priorprob = {}
    condprob = {}
    for c_k in DOC_COUNT_OF_CLASS:
        N_c = DOC_COUNT_OF_CLASS[c_k]
        priorprob[c_k] = (1+N_c)/(len(DOC_COUNT_OF_CLASS)+N)
    for t in TERM_MATRIX:
        for c in DOC_COUNT_OF_CLASS:
            N_tc = TERM_MATRIX[t][c]
            condprob[t][c] = (1+N_tc)/(2+DOC_COUNT_OF_CLASS[c])
    return priorprob, condprob

def classify(DOCUMENT, priorprob, condprob):
    '''DOCUMENT = d_i
    '''
    terms = WordSegment(DOCUMENT)
    max_score = -float('Inf')
    c_k = None
    for c in priorprob:
        score = log(priorprob[c])
        for t in condprob:
            if t in terms:
                score += log(condprob[t][c])
            else:
                score += log(1-condprob[t][c])
        if score > max_score:
            max_score = score
            c_k = c
    return c_k

参考

统计自然语言处理, 宗成庆, 13. 文本分类与情感分类
Introduction to IR, 13. Text classification and Naive Bayes

Yiming Yang,Jan O Pedersen:A comparative Study on Feature Selection in Text Categorization, Proceedings of the Fourteenth International Conference on Machine Learning(ICML~97)，l997 ↩