多模匹配のAC自动机

精确的字符串匹配算法有 单模匹配算法，比如，KMP、BM算法等；和 多模匹配算法，比如，Wu-Manber、AC算法等。

AC算法(Aho-Corasick)是KMP算法向多模式串情形的扩展，该算法使用一种特殊的自动机，即AC自动机。AC自动机由一组模式串P生成，是trie的扩展。

先回顾一下KMP算法。

每读入一个字符，KMP算法更新 既是模式串的前缀、同时也是已读入文本的后缀 的最长字符串的长度。设字符串vβ是下一个 既是模式串p的前缀、同时也是已读入文本t₁…t_i+1的后缀 的最长字符串。可以看出：对模式串当前已匹配前缀u来说，v既是u的一个后缀、也是u的一个前缀，并且字符β一定与t_i+1（即σ）相等。这里，称v是u的一个边界。

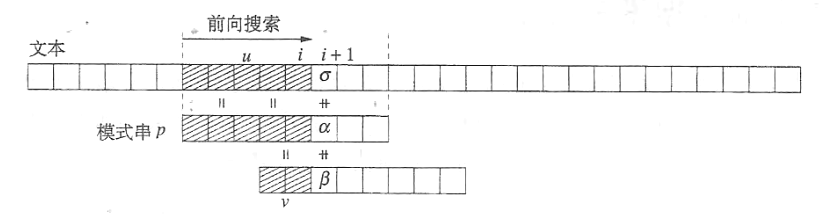
KMP算法：

首先，预处理得到模式串p的每个前缀u的最长边界b(u)=max(v)，即得到所谓的next数组。

然后，设当前文本位置为i，对新读入的字符σ=t_i+1，按照如下步骤计算新的最长前缀：

1. 如果σ=p_|u|+1=α，那么新的最长前缀是up_|u|+1，计算结束；
2. 如果σ≠α，设置u为最长边界b(u)，跳转到步骤1；如果u为空字符，计算结束。

最终，当uσ=p的时候，即匹配完成。

AC算法

AC算法中类似next数组的是一颗改造过的trie树。用q表示模式P对应的trie状态，用L(q)表示从初始状态到q的路径上的标号组成的字符串。S_AC(q)定义为自动机中的另一个状态q’，使得L(q’)是L(q)的最长后缀，这是将“边界”的概念扩展到一组字符串。S_AC(q)称为q的供给状态，称q到S_AC(q)的连线为供给链，称由供给链连接而成的路径为供给路径。初始状态的供给状态为θ。

下图为模式集合P={ATATATA, TATAT, ACGATAT}的AC自动机，虚线为S_AC，双圆圈为终结状态。例如，L(15)=ACGATA，既是它的后缀，同时也是某个模式串(这里是ATATATA)的前缀的最长字符串是ATA，对应状态7，因此S_AC(15)=7。终结状态是那些对应于整个模式串的状态，此外，如果从状态q到根节点的路径上存在终结状态，那么q也是终结状态。例如，由于S_AC(16)是终结状态，所以16也是终结状态。

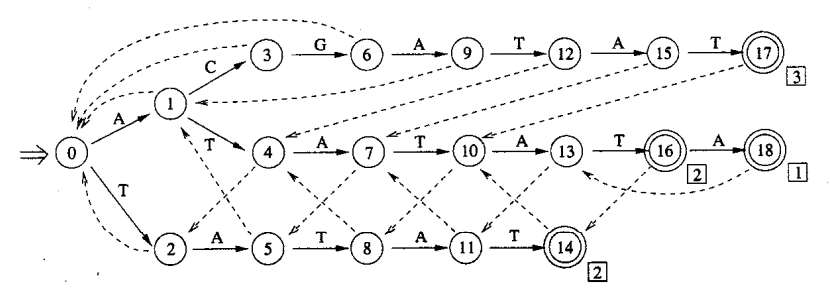
假设已经读入文本t₁…t_i，而既是其后缀、同时也是某个模式串的前缀的最长字符串对应AC自动机的Current状态，记该字符串为v=L(Current)。当读入下一个字符t_i+1并计算t₁…t_it_i+1的新的最长后缀u时，有两种情况：

1. 如果状态Current存在标号为t_i+1的转移，目的状态为f，即δ_AC(Current, t_i+1)=f，那么f将成为新的Current状态。并且，u=L(f)=ut_i+1是t₁…t_it_i+1的最长后缀，同时也是某个模式串的前缀；
2. 如果状态Current不存在标号为t_i+1的转移，那么沿着Current的供给路径回溯，直到：
   • 找到一个状态q，它存在标号为t_i+1的转移。那么q的t_i+1转移的目的状态f成为新的Current状态，并且u=L(f)；
   • 如果到达空状态θ，那么说明要寻找的最大后缀u是空字符串ε，于是从Current跳转到初始状态。

算法伪代码如下，F(Current)表示Current节点所对应的模式P中的相应字符串：

Aho-Corasick(P={p1,...,pr}, T=t1...tn)
    预处理
        AC ← Build_AC(P)
    匹配
        Current ← AC自动机的初始状态
        For pos ∈ 1...n Do
            While δAC(Current, tpos) = θ And SAC(Current) ≠ θ Do
                Current ← SAC(Current)
            End While
            If δAC(Current, tpos) ≠ θ Then
                Current ← AC自动机的初始状态
            End If
            If Current是终结状态 Then
                找到模式串F(Current)
            End If
        End For

预处理阶段，先根据模式串构造trie，然后BFS顺序遍历trie构造S_AC。

假设已经计算出Current之前所有状态的供给函数，现在考虑Current父节点Parent。假设Parent到Current的字符为σ，即Current=δ_AC(Parent, σ)。S_AC(Parent)已经计算出来了，要搜索v=L(Current)的最长后缀u，它同时也对应trie中的一条路径。v可以写成v’σ 的形式，如果u不是空串，那么u一定能写成u’σ 的形式，并且u’一定是v’的后缀。

如果S_AC(Parent)有字符为σ的转移，并且目的状态为h，则w=L(S_AC(Parent))是v’的最长后缀，并且wσ对应trie中的一条路径。wσ就是最长路径u，S_AC(Current)指向h。

如果S_AC(Parent)没有字符为σ的转移，或者抵达空状态θ为止。如果抵达了空状态θ，说明u是空字符串ε，这时将S_AC(Current)置为初始状态。

算法伪代码如下：

Build_AC(P={p1,...,pr})
    AC-trie ← Trie(P)
        δAC是转移函数
    初始节点 ← AC-trie的根节点
    SAC(初始状态) ← θ
    For BFS的Current节点 Do
        Parent ← Current的父节点
        σ ← 从Parent到Current的输入字符
        Down ← SAC(Parent)
        While Down ≠ θ And δAC(Down, σ) = θ Do
            Down ← SAC(Down)
        End While
        If Down ≠ θ Then
            SAC(Current) ← δAC(Down, σ)
            If SAC(Current)是终止节点 Then
                标记Current为终止节点
                F(Current) ← F(Current) ∪ F(SAC(Current))
            End If
        Else
            SAC(Current) ← 初始节点
        End If
    End For

参考

• 柔性字符串匹配