[TOC]
级数
极限、序列的极限、函数的极限、连续
导数、偏导数、微分
设有定义域和取值都在实数域中的函数 y=f(x)。若 f(x) 在点 x0 的某个邻域内有定义,则当自变量 x 在 x0 处取得增量 Δx(点 x0+x 仍在该邻域内)时,相应地函数 y 取得增量 Δy=f(x0+Δx)-f(x)-f(x0);如果 Δy 与 Δx 之比当 Δx→0 时的极限存在,则称函数 y=f(x) 在点 y 与 Δx 之比当Δx→0 时的极限存在,则称函数 y=f(x) 在点 x0 处可导,并称这个极限为函数 y=f(x) 在点 x0 处的导数,记为 f’(x0),即:
\[f'(x_0) = \lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x} = \lim_{\Delta x\to 0}{f(x_0+\Delta x)-f(x_0) \over \Delta x}\]微分也是一种线性描述函数在一点附近变化的方式。
微分和导数是两个不同的概念。但是,对一元函数来说,可微与可导是完全等价的。
可微的函数,其微分等于导数乘以自变量的微分dx,换句话说,函数的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。
函数y = f(x)的微分又可记作dy = f’(x)dx。 在数学中,一个多变量的函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定(相对于全导数,在其中所有变量都允许变化)。函数f关于变量x的偏导数写为 f’x 或者:。
梯度、雅可比矩阵、海森矩阵
- Gradient
- 梯度用于向量微积分(多元函数),即函数f在各个基的方向上的偏导数组成的向量。
- Jacobian
- 对于值为标量的多变量的函数 f(x),我们使用梯度,但是如果是值为向量的多变量的函数(y为向量)怎么办呢?雅克比矩阵实际上是对于梯度的一种泛化。
记m为函数值的维度,记n为变量维度:
- m = 1时,函数的雅克比矩阵就是梯度;
- m = 1而且n=1时,函数的雅克比矩阵和梯度就是简单的导数。
- Hessian
- 某种意义上说,梯度和雅克比矩阵都是一种一阶导数(二者针对的函数的值不同)。二阶导数是什么呢? 一个值为标量的多变量函数的梯度的雅克比矩阵就是二阶导数,也就是Hessian矩阵。
导数和泰勒展开
导数(Derivative)的概念非常基础,在优化理论中求极值一般都搭配泰勒公式使用。
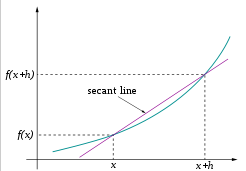
可以看到当$h\to 0$时候,该直线的方向就是导数方向。
一般只用到二阶泰勒展开:
\[f(x) = f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots\]所谓的梯度下降,就是使用一阶泰勒展开,直接沿着梯度方向迭代求解f(x),当f(x)不变时,就求得了极值。
泰勒公式的意义
将复杂的函数近似表达成易于处理的多项式形式。
https://www.coursera.org/learn/single-variable-calculus