FM和FFM算法学习

Posted on |

[TOC]

$\newcommand{\v}{\mathbf{v}} \newcommand{\C}{\mathcal{C}} \newcommand{\x}{\mathbf{x}} \newcommand{\w}{\mathbf{w}} \newcommand{\W}{\mathbf{W}} \newcommand{\V}{\mathbf{V}} \newcommand{\T}{\mathsf{T}} \newcommand{\R}{\mathbb{R}} \newcommand{\N}{\mathbb{N}}$

FM 原理

FM的优点：

  1. 适用于高度稀疏的特征；
  2. 具备线性复杂度，可以训练超大规模数据；

FM对比LR的优点是考虑了任意两个互异特征分量之间的关系。

但是，不同于一次项参数，FM没有直接去估计交互项的参数。因为对观察样本中未出现过的交互特征分量（稀疏数据中很常见），是没法直接去估计相应的参数的。FM的做法是引入辅助向量来表达交互项的参数：

\[\v_i= (v_{i1}, v_{i2}, \cdots, v_{ik})^\T \in \R^k, \quad i=1,2,\cdots,n\]

其中，$k\in \N^+$ 为超参数，并将 $w_{ij}$ 改写为

\[\hat{w_{ij}} = \v_i^\T \v_j := \sum_{l=1}^k v_{il} v_{jl}\]

则FM模型可以表达为：

\[\hat{y}(\x) = w_0+\sum_{i=1}^n w_ix_i + \sum_{i=1}^{n-1}\sum_{j=i+1}^n (\v_i^\T \v_j) x_i x_j\]

可见这里是把原始交互项参数矩阵（交互矩阵）进行了矩阵分解 $\hat{\W} = \V\V^\T$，这也是FM名称的由来。可知矩阵 $\V_{n\times k}$ 是一个$n\times k$维低秩矩阵，$n$是特征维度，$k$是超参数。

原理：当$k$足够大时，对任意对称正定的实矩阵 $\hat{\W} \in \R^{n\times n}$，均存在实矩阵 $\V \in \R^{n\times n}$，使得 $\hat{\W} = \V\V^\T$ 成立。

实际操作中，在高度稀疏数据场景中，由于没有足够的样本来估计复杂的交互矩阵，因此通常超参数 $k$ 取得很小。事实上，对参数$k$的限制，一定程度上也提高了FM模型的泛化能力。

注意：FM既可以用于分类，也可以用于回归。在用于二元分类时，可以使用logloss，同时输出应该经过sigmoid变换（类似Logistic Regression）。

关键思路

原来的二次项参数个数是 $n(n-1)/2$，每个参数 $w_{ij}$ 的训练需要大量 $x_i$ 和 $x_j$ 都非零的样本；由于样本数据本来就比较稀疏，满足“$x_i$ 和 $x_j$ 都非零”的样本将会非常少。

通过引入隐向量，二次项参数个数减少到$kn$。而且参数因子化使得 $x_hx_i$ 的参数和 $x_ix_j$ 的参数不再是相互独立的，因此可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说，$x_hx_i$ 和 $x_ix_j$ 的系数分别为 $\langle \v_h, \v_i \rangle$ 和 $\langle \v_i, \v_j \rangle$，它们之间有共同项 $\v_i$。也就是说，所有包含“$x_i$的非零组合特征”（存在某个 $j\neq i$，使得$x_i x_j \neq 0$）的样本都可以用来学习隐向量 $\v_i$，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中，$w_hw_i$ 和 $w_iw_j$ 是相互独立的。

交互项简化

交互项数量是 $n(n-1)/2$，看上去计算复杂度是 $O(kn^2)$，但其实可以进行简化，使得复杂度降到 $O(kn)$：

\[\sum_{i=1}^{n-1}\sum_{j=i+1}^n (\v_i^\T \v_j) x_i x_j = \frac{1}{2} \sum_{l=1}^k \left( \left(\sum_{i=1}^n v_{il}x_i \right)^2 - \sum_{i=1}^n v_{il}^2 x_i^2 \right)\]

数学原理：利用如公式 $(a+b+c)^2-(a^2+b^2+c^2)$ 求出交叉项。

实例说明

FM第一部分仍然为LR，第二部分是通过两两向量之间的点积来判断特征向量之间和目标变量之间的关系。比如，迪斯尼广告的特征 occupation=Student和City=Shanghai这两个向量之间的角度应该小于90，它们之间的点积应该大于0，说明和迪斯尼广告的点击率是正相关的。这种算法在推荐系统领域应用比较广泛。

libfm

示例，如何把MovieLens的评分数据转换成libSVM格式的数据：

https://thierrysilbermann.wordpress.com/2015/02/11/simple-libfm-example-part1/

FM的优化方法

优化问题：

\[\Theta = \arg\min_\Theta \sum_{i=1}^N\left( loss\left(\hat{y}(\x^{(i)}), y^{(i)}\right) + \sum_{\theta\in\Theta}\lambda_\theta\theta^2\right)\]

模型各参数的梯度：

\[\frac{\partial}{\partial\theta} y (\x) = \left\{ \begin{array}{ll} 1, & \text{if}\; \theta\; \text{is}\; w_0 \\ x_i, & \text{if}\; \theta\; \text{is}\; w_i \\ x_i \sum_{j=1}^n v_{j, f} x_j - v_{i, f} x_i^2, & \text{if}\; \theta\; \text{is}\; v_{i, f} \end{array}\right.\]

FM的参数集$\Theta$通常很大，为了避免正则化系数过多，可以对其分组，每组中的参数使用同一个正则化系数：$w_0$为一组，$w_1,w_2,\cdots,w_n$按照特征分量的含义分成$\Pi$，则相应正则化系数集$\lambda$ 就是

\[\lambda^0, \lambda_{\pi(i)}^w, \lambda_{pi(i),j}^v, \quad i\in \brace{i,2,\cdots,n}, j \in \brace{1,2,\cdots,k}\]

其中，$\pi(i)$ 表示参数$w_i$被分在第 $\pi(i) \in \brace{1,2,\cdots,\Pi}$ 组。

SGD

FM SGD

输入：训练集 $S$，正则化系数集 $\lambda$，学习率 $\eta$，正态分布方差 $\sigma$ 输出：模型参数 $\Theta = (w_0, \w, \V)$

  1. for $(\x,y) \in S$
  2. 　　$w_0 =w_0 - \eta \left({\partial loss(\hat{y}(\x),y) \over \partial w_0} + 2\lambda^0w_0\right)$
  3. 　　for $i \in \brace{1,2,\cdots,n}$
  4. 　　　　$w_i =w_i - \eta \left({\partial loss(\hat{y}(\x),y) \over \partial w_i} + 2\lambda_{\pi(i)}^ww_i\right)$
  5. 　　　　for $j \in \brace{1,2,\cdots,k}$
  6. 　　　　　　$v_{ij}=v_{ij}-\eta \left({\partial loss(\hat{y}(\x),y) \over \partial v_{ij} } + 2\lambda_{\pi(i),j}^vv_{ij}\right)$

若干实现：

  • http://blog.csdn.net/google19890102/article/details/45532745
  • https://gist.github.com/qxj/80984f74f3b9d3447fa3e131cb495ece
  • https://github.com/blebreton/spark-FM-parallelSGD
  • https://github.com/coreylynch/pyFM

FFM

FFM（Field-aware Factorization Machines）引入field的概念，相同性质的特征归入同一个field。这样在FFM里每一维特征$x_i$，针对其他特征的每一种field $f_j$，都会学习一个隐向量 $\v_{i,f_j}$。因此，隐向量不仅与特征有关，也与field有关。

比如，特征$x_i$分别与特征$x_j$和$x_k$交互（假设后俩特征分别属于不同的feild $f_j$和$f_k$），原来在FM里，都是使用同样的隐向量$\v_i$；但在FFM里，会使用不同的隐向量$\v_{i,f_j}$和$\v_{i,f_k}$，这就是FFM和FM的唯一区别。

\[\hat{y}(\x) = w_0+\sum_{i=1}^n w_ix_i + \sum_{i=1}^{n-1}\sum_{j=i+1}^n (\v_{i,f_j}^\T \v_{j,f_i}) x_i x_j\]

其中，$f_j$ 是第 $j$ 个特征所属的field。如果隐向量的长度为 $k$，那么FFM的二次参数有 $nfk$ 个，远多于FM模型的 $nk$ 个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是 $O(kn^2)$。

libffm算法

这个版本省略了常数项和一次项，且采用logloss和L2只能用于二分类问题：

\[\phi(\w, \x) = \sum_{j_1, j_2 \in \C_2} \langle \w_{j_1, f_2}, \w_{j_2, f_1} \rangle x_{j_1} x_{j_2}\]

输入：样本特征数量 $tr.n$、field的个数 $tr.m$、训练参数 $pa$（$pa.norm$ 表示是否要归一化特征）

关键步骤：

  1. 计算每个样本的FFM项，即上式 $\phi$；
  2. 计算每一个样本的训练误差$L_{tr}$，如算法所示，这里采用的是交叉熵损失函数 $\log(1+e\phi)$；
  3. 利用单个样本的损失函数计算梯度 $g_\Phi$，再根据梯度更新模型参数

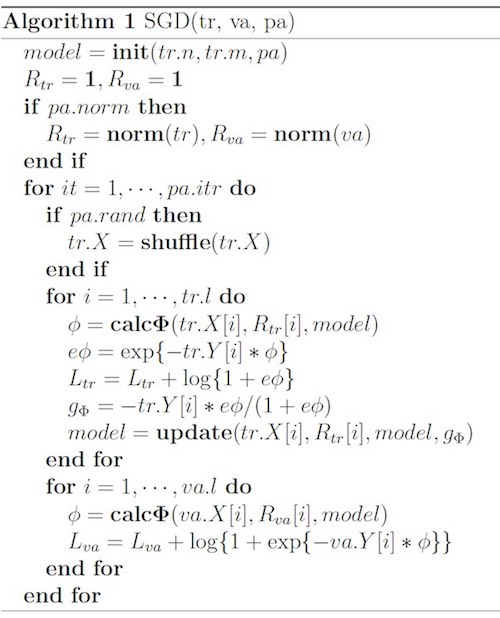
FFM SGD

疑问：正则项在哪里？在计算$\phi$的公式里。

FNN

参考：用户在线广告点击行为预测的深度学习模型（含PPT下载） 张伟楠

因为DNN并不适合处理非常高维度的特征（会导致需要拟合的参数过多），我们需要将非常大的特征向量嵌入到低维向量空间中来减小模型复杂度，而FM无疑是被业内公认为最有效的embedding model。大量高维稀疏特征经过FM embedding后再接入DNN，即FNN。

参考