FTRL算法学习

Posted on |

[TOC]

要解决的问题：在Online Learning中L1也不能保证参数的稀疏性。

Online不同于Batch，Online中每次参数的更新并不是沿着全局梯度进行下降，而是沿着某个样本的产生的梯度方向下降，整个寻优过程变得像是一个“随机”查找的过程（SGD中Stochastic的来历），这样Online最优化求解即使采用L1正则化的方式，也很难产生稀疏解。

之前的工作：简单截断、TG、FOBOS、RDA。 FTRL：训练精度 + 稀疏性，都最佳。

简单截断

最intuitive的方法，直接设定一个阈值，当参数某一维度的系数小于该阈值时，则设置为0。

Cons：实际中，如OGD，参数的某个系数比较小也可能是因为训练样本不足（尤其训练刚开始时），简单截断会造成这部分特征的丢失。

算法：每训练$k$个数据对参数做一次截断置零：

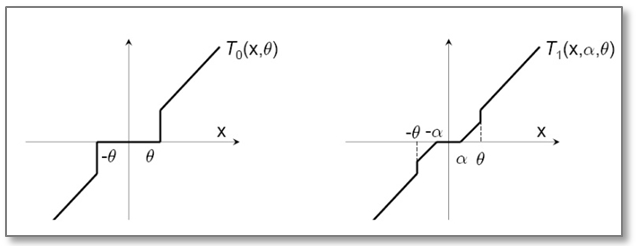
\[f(w_i)=T_0\left(w_i-\eta \nabla L(w_i,z_i),\theta \right) \\ T_0(v_j,\theta )=\left\{\begin{matrix} 0 & \text{if} \left | v_j \right |\leq \theta\\ v_j & \text{otherwise} \end{matrix}\right.\]

TG (Truncated Gradient)

对简单截断思路做了一点改进：

\[f(w_i)=T_1\left(w_i-\eta \nabla L(w_i,z_i), \eta \lambda_i,\theta \right) \\ T_1(v_j,\alpha ,\theta )=\left\{\begin{matrix} \max(0,v_j-\alpha ) & \text{if}\ v_j\in [0,\theta ]\\ \min(0,v_j+\alpha ) & \text{if}\ v_j\in [-\theta, 0]\\ v_j & \text{otherwise} \end{matrix}\right.\]

可以通过 $\lambda$ 和 $\theta$ 来控制稀疏性，这俩值越大越稀疏。

简单截断和TG的区别在于采用了不同的截断公式$T_0$和$T_1$，如图所示：

Truncated gradient

FOBOS (Forward-Backward Splitting)

FOBOS可以看作TG的一种特殊形式。

FOBOS把每步迭代分解成两部分：

  • emprical loss sgd
  • 最优化问题

而最优化问题又分为两部分：

  • 2范数保证不能离第一步loss迭代结果太远（regret bound?）
  • 正则项
\[\begin{aligned} w_{t+\frac12} &=w_t-\eta_t g_t \\ w_{t+1} &= \arg\min_w \left\{\frac12 \Abs{w-w_{t+\frac12}}^2 + \eta_{t+\frac12} r(w)\right\} \end{aligned}\]

RDA (Regularized Dual Averaging)

L. Xiao. Dual averaging method for regularized stochastic learning and online optimization. NIPS, 2009

微软2009年论文，能较好地在精度与稀疏性间进行权衡。

FTRL (Follow the Regularized Leader)

FTL：每次找到让之前所有loss之和最小的参数，使得累积regret最小。

\[w_{t+1} = \arg\min_w \sum_{i=1}^t f_i(w)\]

其中，$f_i$是第$i$轮的loss。

SGD：

\[w_{t+1} = w_t - \eta g_t\]

FTRL-Proximal：

\[w_{t+1} = \arg\min_w\left(g_{1:t} \cdot w+\frac12\sum_{s=1}^t\sigma_s\Abs[2]{w-w_s}^2+\lambda_1\Abs[1]{w}\right)\]

其中，$g_{1:t}=\sum_{i=1}^tg_i$ 是梯度的累积。

整个式子说明：

  • 第一项是对loss贡献的一个估计；
  • 第二项控制模型$w$在每次迭代中变化不要太大（proximal?），$\sigma_s$表示学习率；
  • 第三项代表L1正则（稀疏解）。

上式有解析解，具体推导过程可以参考新浪冯扬的文章。

FTRL结合了FOBOS和RDA的优点，并且能针对不同维度单独进行训练。

FTRL Algorithm

四个参数$\alpha$、$\beta$、$\lambda_1$和$\lambda_2$的设置可以参考FTRL论文里的建议。

FTRL结合了L1和L2正则，不过这里L2并未影响稀疏性。

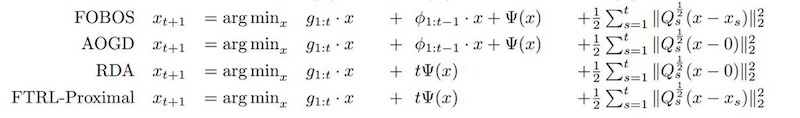
FTRL L1/L2

Per-coordinate learning rate和adagrad思路类似，都是在分母在累加历史梯度RMS来自适应不同维度的学习率。但由于学习率是non-increasing的，长期训练可能影响regret？

代码实现

lr sgd

from math import exp, log, sqrt
from sklearn import metrics
import random
import math

# hyper-parameters
alpha = 0.005  # learning rate

# feature/hash trick
D = 160000     # number of weights to use

# training/validation
epoch = 1      # learn training data for N passes
holdout = 100  # use every N training instance for holdout validation

threshold = 0.5

class lr_sgd(object):
    def __init__(self, alpha, D):
        self.alpha = alpha  # 学习率
        self.w = [0.] * D   # D是特征纬度

    def predict(self, x):
        wTx = 0.
        for i in x.iterkeys():
            wTx += self.w[i] * x[i]
        return 1. / (1. + exp(-max(min(wTx, 35.), -35.)))  # sigmoid

    def update(self, x, p, y):
        g = p - y
        for i in x.iterkeys():
            g = (p - y) * x[i]  # 第i维参数的梯度 g = (py - y) * x[i]
            self.w[i] = self.w[i] - self.alpha * g


def logloss(p, y):
    p = max(min(p, 1. - 10e-15), 10e-15)
    return -log(p) if y == 1. else -log(1. - p)


def data(path, D, sampling=False):
    counter = 0
    for line in open(path):
        # 解析并返回样本
        yield counter, x, y


# 开始训练
learner = lr_sgd(alpha, D)

for e in xrange(epoch):
    loss = 0.
    count = 0

    for t, x, y in data(train, D, True):
        # step 1, get prediction from learner
        p = learner.predict(x)

        if t % holdout == 0:  # validation
            loss += logloss(p, y)
            count += 1
        else:
            # step 2-2, update learner with label (click) information
            learner.update(x, p, y)

        if t % 50000 == 0 and t > 1:
            print('encountered: %d\tcurrent logloss: %f' % (t, loss/count))

    print('Epoch %d finished, holdout logloss: %f' % (e, loss/count))


# 测试集
y_true = []
y_pred = []
t = 0
for t, x, y in data(test, D):
    p = learner.predict(x)
    y_true.append(y)
    y_pred.append(p)
    t += 1

print "total auc=%.6f" % (metrics.roc_auc_score(y_true, y_pred))

lr ftrl

把lr sgd的lr_sgd算法替换成ftrl_proximal即可，其他逻辑不变。

# hyper-parameters
alpha = 0.1    # learning rate
beta = 1.      # smoothing parameter for adaptive learning rate
L1 = 1.        # L1 regularization, larger value means more regularized
L2 = 1.        # L2 regularization, larger value means more regularized

# feature/hash trick
D = 160000     # number of weights to use

class ftrl_proximal(object):
    def __init__(self, alpha, beta, L1, L2, D):
        self.alpha = alpha
        self.beta = beta
        self.L1 = L1
        self.L2 = L2

        self.D = D

        self.n = [0.] * D  # n: squared sum of past gradients
        self.z = [0.] * D  # z: weights
        self.w = [0.] * D  # w: lazy weights

    def predict(self, x):
        wTx = 0.
        for i in x.iterkeys():
            sign = -1. if self.z[i] < 0 else 1.
            # build w on the fly using z and n, hence the name - lazy weights -
            if sign * self.z[i] <= self.L1:
                self.w[i] = 0.  # w[i] vanishes due to L1 regularization
            else:
                self.w[i] = (sign * self.L1 - self.z[i]) / ( (self.beta + sqrt(self.n[i]))/self.alpha + self.L2 )
            wTx += self.w[i] * x[i]
        return 1. / (1. + exp(-max(min(wTx, 35.), -35.)))  # bounded sigmoid

    def update(self, x, p, y):
        for i in x.iterkeys(): # update z and n
            g = (p - y) * x[i]
            sigma = (sqrt(self.n[i] + g * g) - sqrt(self.n[i])) / self.alpha
            self.z[i] += g - sigma * self.w[i]
            self.n[i] += g * g

参考