卡方检验
类别资料的分析上,常用卡方检验(Chi-square test)。
卡方检验的原理:检验观察到的次数分布是否与期望的次数分布相复合。因此,检验结果只有“是”与“否”两种情况,所以卡方检验一般都视为单尾的检验。
离散随机变量属于各类别的期望次数是:$E_i=np_i$, 其中,n为样本数,$p_i$是属于第i类的概率。
直觉上,只要计算类别i的观察次数$O_i$与期望次数$E_i$的残差(residual),即可以衡量类别i的观察次数与期望次数的相符程度,残差值越大,则越不相符。于是就得到了卡方分布的公式:
\[\chi^2 = \sum_{i=1}^k{(O_i-E_i)^2 \over E_i}, \qquad i=1,\cdots,k\]【疑惑】这里参考了《生物统计学》10. 卡方分布,和之前学到卡方分布的定义有点偏差?
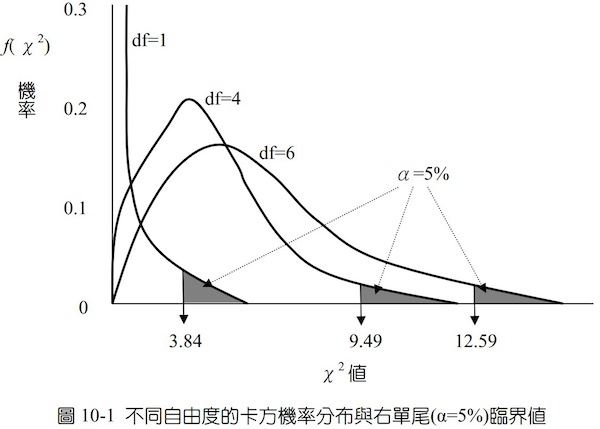
适合度检验(goodness of fit test)
利用样本检验母体分布是否为某一特定分布。
例如:掷骰子300次出现各点的次数分布,判断该骰子是否为公平骰子?($\alpha=0.01$)
| 点数 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 次数 | 33 | 61 | 49 | 65 | 55 | 37 |
同质性检验
检验两个或两个以上母体的某一特征的分布是否相近。
例如:某项民意测验调查甲、乙两地区居民是否支持劳动法,自甲地区抽出300人,乙地区抽出250人,调查结果如下:
| 支持 | 反对 | 无意见 | |
|---|---|---|---|
| 甲地区 | 158 | 105 | 37 |
| 乙地区 | 119 | 94 | 37 |
独立性检验(independent test)
检验两个自变量之间是否独立(没有交互作用 interaction)。
例如:学校为了解男女学生对两性共用厕所的意见,100位男女学生的意见如下,请问该问题的意见是否随男女性别而不同?
| / | 赞成 | 反对 | 合计 |
|---|---|---|---|
| 男 | 44 | 16 | 60 |
| 女 | 16 | 24 | 40 |
| 合计 | 60 | 40 | 100 |
参考
- 《数理统计学教程》陈希孺,3. 假设检验
- 《统计学》Freedman 28. 卡方检验