拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。前提是:只有当目标函数为凸函数时,使用这两种方法才保证求得的是最优解。
$\newcommand{\R}{\mathbb{R}}$
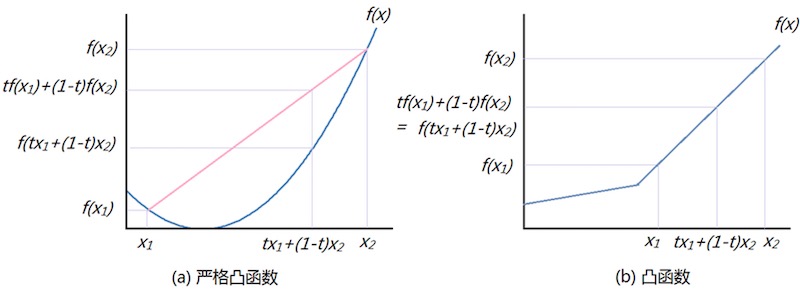
凸函数
如果$f(X)$是定义在$N$维向量空间上的实值函数,对在$f(X)$的定义域$\R^N$上的任意两点$X_1$和$X_2$,以及任意$[0,1]$之间的值$t$都有:
\[f(tX_1 + (1-t)X_2) \geq tf(X_1)+(1-t)f(X_2), \quad \forall X_1,X_2 \in \R^N, 0\leq t\leq 1\]那么称 $f(X)$ 是凸函数。如果去掉等于的情况,则是严格凸函数(Strict Convex)。
三种凸优化问题:无约束优化、等式约束优化和不等式约束优化。
针对无约束最优化问题,通常做法就是对$f(X)$求导,并令$\frac{\partial f(X)}{\partial X}=0$,求解可以得到最优值。如果$f(X)$为凸函数,则可以保证结果为全局最优解。而等式约束和不等式约束的最优化问题需要分别使用拉格朗日乘子法和KKT条件转化成无约束优化问题求解。
拉格朗日乘子法(Lagrange Multiplier)
等式约束优化问题:
\[X = \arg\min_X f(X) \\ s.t.\quad h_k(X)=0 \quad k=1,2,\cdots,n\]含义是在$n$个等式约束的条件下,求解$X$,令目标函数$f(X)$最小。通过拉格朗日系数把等式约束和目标函数组合成为一个式子,对该式进行最优化求解:
\[X = \arg\min_X \left[ f(X) + A^T H(X) \right]\]其中,$A=[a_1,a_2,\cdots,a_n]^T \in R^n$,$H(X)=[h_1(X),h_2(X),\cdots,h_n(X)]^T \in \R^n$。
KKT条件
对不等式约束到等式约束的转换技巧是引入两个 松弛变量 $a^2$ 和 $b^2$ 利用平方项大于等于0,得到Lagrang等式。
不等式约束优化问题描述:
\[X = \arg\min_X f(X) \\ s.t.\quad h_k(X)=0 \quad k=1,2,\cdots,n; \quad g_l(x)\leq 0 \quad l=1,2,\cdots,m\]含义是在$n$个等式约束 和 $m$个不等式约束的条件下,求解$x$,令目标函数$f(x)$最小。同样,通过KKT条件把 等式约束、不等式约束 和 目标函数 组合成为一个式子,对该式进行最优化求解:
\[L(X,A,B) =f(X) + A^T H(X) +B^T G(X)\]KKT条件是说最优值必须满足以下条件:
\[\frac{\partial}{\partial X}L(X,A,B) = 0 \\ H(X) = 0 \\ B^TG(X) = 0\]其中,$B(X)=[b_1,b_2,\cdots,b_m]^T \in \R^m$,$G(X)=[g_1(X),g_2(X),\cdots,g_m(X)]^T \in \R^m$。
KKT条件中,$B^TG(X)=0$ 这个条件最有趣,因为 $g_l(X)\leq 0$,如果满足这个等式,则需要 $b_l=0$ 或 $g_l=0$。
参考
- http://www.wbrecom.com/?p=264
- 《线性规划》张建中 3.1 KKT条件