主题模型之LDA

$\newcommand{\X}{\mathcal{X}} \newcommand{\a}{\vec{\alpha}} \newcommand{\b}{\vec{\beta}} \newcommand{\p}{\vec{p}} \newcommand{\w}{\vec{w}} \newcommand{\x}{\vec{x}} \newcommand{\z}{\vec{z}} \newcommand{\vt}{\vec{\vartheta}} \newcommand{\vp}{\vec{\varphi}}$

[TOC]

在原始的pLSA模型中，我们求解出两个参数：“主题-词项”矩阵 $\Phi$ 和“文档-主题”矩阵 $\Theta$ ，但是我们并未考虑参数的先验知识；而LDA的改进之处，是对这俩参数之上分别增加了先验分布，相应参数称作超参数(hyperparamter)。概率图表示如下：

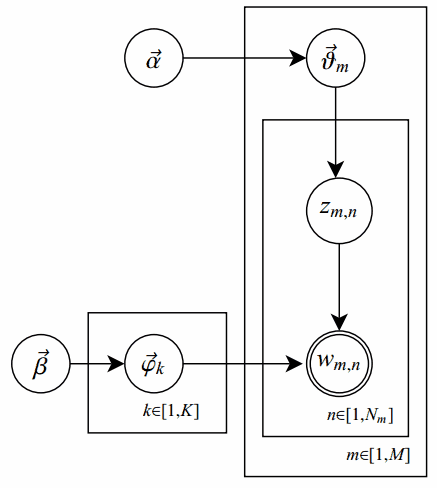
其中，单圆圈表示隐变量；双圆圈表示观察到的变量；把节点用方框(plate)圈起来，表示其中的节点有多种选择。所以这种表示方法也叫做plate notation，具体可参考PRML 8.0 Graphical Models。

对应到上图，只有 $w_{m,n}$ 是观察到的变量，其他都是隐变量或者参数，其中 $\a$ 和 $\b$ 是超参数；方框中， \(\Phi = \brace{\vp_k}_{k=1}^K\) 表示有 $K$ 种“主题-词项”分布； \(\Theta=\brace{\vt_m}_{m=1}^M\) 有 $M$ 种“文档-主题”分布，即对每篇文档都会产生一个 $\vt_m$ 分布；每篇文档 $m$ 中有 $n$ 个词，每个词 $w_{m,n}$ 都有一个主题 $z_{m,n}$ ，该词实际是由 $\vp_{z_{m,n}}$ 产生。具体生成过程下面再说。

贝叶斯估计

在pLSA原参数之上增加先验分布，其实就是用贝叶斯估计取代最大似然估计，具体要了解各种参数估计方法可以参考Heinrich论文的第二部分。简单说，最大似然估计(MLE)和最大后验估计(MAP)都是把待估计的参数看作一个拥有固定值的变量，只是取值未知。通常估计的方法都是找使得相应的函数最大时的参数；由于MAP相比于MLE会考虑先验分布的影响，所以MAP也会有超参数，它的超参数代表的是一种信念(belief)，会影响推断(inference)的结果。比如说抛硬币，如果我先假设是公平的硬币，这也是一种归纳偏置(bias)，那么最终推断的结果会受我们预先假设的影响。贝叶斯估计是对MAP的扩展，但它不再对参数做直接的估计，而是把待估计的参数看作服从某种分布的随机变量。根据贝叶斯法则：

\[{\rm posterior = {likelihood \cdot prior \over evidence} }\]

即

\[p(\vartheta|\X) = {p(\X|\vartheta) \cdot p(\vartheta) \over p(\X)}\]

在MLE和MAP中，由于是要求函数最大值时的参数，所以都不会考虑evidence。但在贝叶斯估计中，不再直接取极值，所以还会考虑evidence，下面的这个积分也是通常贝叶斯估计中最难处理的部分：

\[p(\X) = \int_{\vartheta \in \Theta} p(\X|\vartheta) p(\vartheta) \mathrm{d}\vartheta\]

evidence相当于对所有的似然概率积分或求和(离散时)，所以也称作边界似然。

共轭先验

由于有积分的存在，贝叶斯估计常常会很难推算，这里我们就需要利用一种共轭先验(Conjugate Prior)的数学知识。在贝叶斯统计理论中，如果某个随机变量 $\vartheta$ 的先验分布 $p(\vartheta)$ 和后验分布 $p(\vartheta\vert\X)$ 属于统一分布簇(也就是说有同样的函数形式)，则称先验分布 $p(\vartheta)$ 和后验分布 $p(\vartheta\vert\X)$ 为共轭分布，先验分布 $p(\vartheta)$ 是似然函数 $p(\X\vert\vartheta)$ 的共轭先验。

由于pLSA中参数 $\Phi$ 和 $\Theta$ 都服从多项分布，因此选择Dirichlet分布作为他们的共轭先验。在pLSA中，假设这俩多项分布是确定的，我们在已经假设确定的分布下，选择具体的主题和词项；但在LDA中，这俩多项分布的参数是被当作随机变量，服从另一层先验分布，所以，Dirichlet分布也称作分布的分布，其定义如下：

\[\begin{align} \mathrm{Dir}(\p|\a) &\triangleq {\Gamma \left(\sum_{k=1}^K \alpha_k \right) \over \prod_{k=1}^K \Gamma(\alpha_k)} \prod_{k=1}^K p_k^{\alpha_k -1} \tag 1 \\ &\triangleq \frac{1}{\Delta(\a)} \prod_{k=1}^K p_k^{\alpha_k -1} \end{align}\]

其中， $\p$ 是要猜测的随机向量， $\a$ 是超参数， $\Delta(\a)$ 称作Delta函数，可以看作Beta函数的多项式扩展，是Dirichlet分布的归一化系数，定义如下：

\[\Delta(\a) = {\prod_{k=1}^{\mathrm{dim} \a} \Gamma(\alpha_k) \over \Gamma \left( \sum_{k=1}^{\mathrm{dim} \a} \alpha_k \right)} = int \prod_{k=1}^V p_k^{\alpha_k -1} \mathrm{d}\p \tag 2\]

相应的多项分布定义：

\[\mathrm{Mult}(\vec{n}|\p, N) \triangleq {N \choose \vec{n}} \prod_{k=1}^K p_k^{n_k} \tag 3\]

其中， $\p$ 和 $\vec{n}$ 服从约束 $\sum_k p_k=1$ 和 $\sum_k n_k = N$ 。

由于 $\Gamma(x+1) = x!$ 就是阶乘在实数集上的扩展，显然，公式(1)和(3)有相同的形式，所以，这俩分布也称作Dirichlet-Multinomail共轭。

如果 $\p \sim \mathrm{Dir}(\p\vert\a)$ ，则 $\p$ 中的任一元素 $p_i$ 的期望是：

\[\begin{align} E(p_i) &=\int^1_0 p_i\cdot \mathrm{Dir}(\p|\a)\mathrm{d}p \\ &={\Gamma \left(\sum^K_{k=1}\alpha_k \right) \over \Gamma(\alpha_i)} \cdot {\Gamma(\alpha_i+1) \over \Gamma \left(\sum^K_{k=1}\alpha_k+1 \right)} \\ &={\alpha_i \over \sum^K_{k=1}\alpha_k} \tag 4 \end{align}\]

可以看出，超参数 $\alpha_k$ 的直观意义就是事件先验的伪计数(prior pseudo-count)。

LDA生成模型

在LDA中，“文档-主题”向量 $\vt_m$ 由超参数为 $\a$ 的Dirichlet分布生成，“主题-词项”向量 $\vp_k$ 由超参数为 $\b$ 的Dirichlet分布生成，根据概率图，整个样本集合的生成过程如下：

• 对所有的主题 $k \in [1,K]$ (生成 $\Phi$ ， $K \times N$ 矩阵)：
  • 生成“主题-词项”分布 $\vp_k \sim \mathrm{Dir}(\b)$ ( $N$ 维矩阵，对应词表 $\mathcal{V}$ 中的每个词项的概率)
• 对所有的文档 $m \in [1,M]$ ：
  • 生成当前文档 $m$ 相应的“文档-主题”分布 $\vt_m \sim \mathrm{Dir}(\a)$ ( $K$ 维向量，即第 $m$ 篇文档对应的每个主题的概率)
  • 生成当前文档 $m$ 的长度 $N_m \sim \mathrm{Poiss(\xi)}$
  • 对当前文档 $m$ 中的所有词 $n \in [1, N_m]$ ：
    • 生成当前位置的词的所属主题 $z_{m,n} \sim \mathrm{Mult}(\vt_m)$
    • 根据之前生成的主题分布 $\Phi$ ，生成当前位置的词的相应词项 $w_{m,n} \sim \mathrm{Mult}(\vp_{z_{m,n}})$

由该生成过程可知，第 $m$ 篇文档中第 $n$ 个词 $t$ 的生成概率：

\[p(w_{m,n}=t|\vt_m, \Phi) = \sum_{k=1}^K p(w_{m,n}=t|\vp_k) p(z_{m,n}=k|\vt_m)\]

其中， $\Phi = \brace{\vp_k}_{k=1}^K$ 。

根据所有已知信息和带超参数的隐变量，我们可以写出联合分布：

\[p(\w_m,\z_m,\vt_m,\Phi|\a,\b) = \overbrace{ \underbrace{ \prod_{n=1}^{N_m} p(w_{m,n}|\vp_{z_{m,n}})p(z_{m,n}|\vt_m) }_\text{word plate} \cdot p(\vt_m|\a) }^\text{document plate (1 document)} \cdot \underbrace{ p(\Phi|\b) }_\text{topic plate}\]

通过对 $\vt_m$ 和 $\Phi$ 积分以及 $z_{m,n}$ 求和，可以求得 $\w_{m,n}$ 的分布：

\[\begin{align} p(\w_m|\a,\b) &= \int \int p(\vt_m|\a) \cdot p(\Phi|\b) \cdot \prod_{n=1}^{N_m} \sum_{z_{m,n}} p(w_{m,n}|\vp_{z_{m,n}}) p(z_{m,n}|\vt_m) \mathrm{d}\Phi \mathrm{d}\vt_m \\ &= \int\int p(\vt_m|\a) \cdot p(\Phi|\b) \cdot \prod_{n=1}^{N_m} p(w_{m,n}|\vt_m,\Phi) \mathrm{d}\Phi \mathrm{d}\vt_m \end{align}\]

整个样本的分布：

\[p(\mathcal{W}|\a,\b) = \prod_{m=1}^M p(\w_m|\a,\b)\]

符号解释：

• $M$ 文档数(固定值)
• $K$ 主题(component)数(固定值)
• $V$ 词项数(固定值)
• $\a$ “文档-主题”分布的超参数( $K$ 维向量，如果对称(symmetric)参数，则是一个标量)
• $\b$ “主题-词项”分布的超参数( $V$ 维向量，如果对称参数，则是一个标量)
• $\vt_m$ 对于文档 $m$ 的主题分布参数标记 $p(z\vert d=m)$ ，每篇文档均不同， $\Theta=\brace{\vt_m}_{m=1}^M$ 是一个 $M \times K$ 矩阵
• $\vp_m$ 对于主题 $k$ 的词项分布参数标记 $p(t\vert z=k)$ ，每个主题均不同， $\Phi=\brace{\vp_k}_{k=1}^K$ 是一个 $K \times V$ 矩阵
• $N_m$ 文档 $m$ 的长度，这里由Poisson分布决定
• $z_{m,n}$ 文档 $m$ 中第 $n$ 个词所属的主题
• $w_{m,n}$ 文档 $m$ 中第 $n$ 个词的词项

Gibbs Sampling

Blei的原始论文使用变分法(Variational inference)和EM算法进行贝叶斯估计的近似推断，但不太好理解，并且EM算法可能推导出局部最优解。Heinrich使用了Gibbs抽样法，这也是目前LDA的主流算法。

通常均匀分布 $\mathrm{Uniform}(0,1)$ 的样本，即我们熟悉的类rand()函数，可以由线性同余发生器生成；而其他的随机分布都可以在均匀分布的基础上，通过某种函数变换得到，比如，正态分布可以通过Box-Muller变换得到。然而，这种变换依赖于计算目标分布的积分的反函数，当目标分布的形式很复杂，或者是高维分布时，很难简单变换得到。

当一个问题无法用分析的方法来求精确解，此时通常只能去推断该问题的近似解，而随机模拟(MCMC)就是求解近似解的一种强有力的方法。随机模拟的核心就是对一个分布进行抽样(Sampling)。随机模拟也可用于类pLSA算法，但现在很少有人这么做。

MCMC的基础：Markov链通过转移概率矩阵可以收敛到稳定的概率分布。这意味着MCMC可以借助Markov链的平稳分布特性模拟高维概率分布 $p(\x)$ ；当Markov链经过burn-in阶段，消除初始参数的影响，到达平稳状态后，每一次状态转移都可以生成待模拟分布的一个样本。Gibbs抽样是MCMC的一个特例，它交替的固定某一维度 $x_i$ ，然后通过其他维度 $\x_{\neg{i}}$ 的值来抽样该维度的值。它的基本算法如下：

1. 选择一个维度 $i$ ，可以随机选择；
2. 根据分布 $p(x_i\vert\x_{\neg{i}})$ 抽样 $x_i$ 。

所以，如果要完成Gibbs抽样，需要知道如下条件概率：

\[p(x_i|\x_{\neg{i}}) = {p(\x) \over p(\x_{\neg{i}})} = {p(\x) \over \int p(\x)\mathrm{d}x_i}, \quad \x = \brace{x_i,\x_{\neg{i}}}\]

如果模型包含隐变量 $\z$ ，通常需要知道后验概率分布 $p(\z\vert\x)$ ，所以，包含隐变量的Gibbs抽样器公式如下：

\[p(z_i|\z_{\neg{i}}, \x) = {p(\z,\x) \over p(\z_{\neg{i}},\x)} = {p(\z,\x) \over \int_Z p(\z,\x)\mathrm{d}z_i} \tag 5\]

LDA Gibbs Sampler

为了构造LDA Gibbs抽样器，我们需要使用隐变量的Gibbs抽样器公式。在LDA模型中，隐变量为 $z_{m,n}$ ，即样本中每个词 $w_{m,n}$ 所属的主题，而参数 $\Theta$ 和 $\Phi$ 等可以通过观察到的 $w_{m,n}$ 和相应的 $z_{m,n}$ 积分求得，这种处理方法称作collapsed，在Gibbs sampling中经常使用。

下面给出要推断的目标分布，它和联合分布成正比：

\[p(\z|\w) = {p(\z,\w) \over p(\w)} = {\prod_{i=1}^W p(z_i,w_i) \over \prod_{i=1}^W \sum_{k=1}^K p(z_i=k,w_i)}\]

这里省略了超参数，这个分布涉及很多离散随机变量，并且分母是 $K_W$ 个项的求和，很难求解。此时，就需要Gibbs sampling发挥用场了，我们期望Gibbs抽样器可以通过Markov链利用全部的条件分布 $p(z_i\vert\z_{\neg{i}},\w)$ 来模拟 $p(\z\vert\w)$ 。根据公式(4)，我们需要写出联合概率分布 $p(\w,\z)$ ：

\[p(\w,\z|\a,\b) = p(\w|\z,\b)p(\z|\a)\]

由于此公式第一部分独立于 $\a$ ，第二部分独立于 $\b$ ，所以可以分别处理。

第一部分，可以由观察到的词数以及相应主题的多项分布产生：

\[p(\w|\z,\Phi) = \prod_{i=1}^W p(w_i|z_i) = \prod_{i=1}^W \varphi_{z_i,w_i}\]

由于样本中的 $W$ 个词服从参数为主题 $z_i$ 的独立多项分布，这意味着，我们可以把上面的对词的乘积分解成对主题和对词项的两层乘积：

\[p(\w|\z,\Phi) = \prod_{k=1}^K \prod_{\brace{i:z_i=k}}p(w_i=t|z_i=k) = \prod_{k=1}^K \prod_{t=1}^V \varphi^{n^{(t)}_k}_{k,t} \tag 6\]

其中， $n_k^{(t)}$ 是词项 $t$ 在主题 $k$ 中出现的次数。目标分布 $p(\w\vert\z,\b)$ 需要对 $\Phi$ 积分，根据 $\Delta(\a)$ 函数公式(2)可得：

\[\begin{align} p(\w|\z,\b) &= \int p(\w|\z,\Phi) p(\Phi|\b) \mathrm{d}\Phi \\ &= \int \prod_{z=1}^K {1 \over \Delta(\b)} \prod_{t=1}^V \varphi_{z,t}^{n_z^{(t)}+\beta_t-1} \mathrm{d} \vp_z \\ &= \prod_{z=1}^K {\Delta(\vec{n}_z + \b) \over \Delta(\b)}, \quad \vec{n}_z = \brace{n_z^{(t)}}_{t=1}^V \end{align}\]

这个结果可以看作 $K$ 个Dirichlet-multinomial模型的乘积。

第二部分，类似于 $p(\w\vert\z,\b)$ 的步骤，先写出条件分布，然后分解成两部分的乘积：

\[p(\z|\Theta) = \prod_{i=1}^W p(z_i|d_i) = \prod_{m=1}^M\prod_{k=1}^K p(z_i=k|d_i=m) = \prod_{m=1}^M\prod_{k=1}^K \theta_{m,k}^{n_m^{(k)}} \tag 7\]

其中， $d_i$ 是单词 $i$ 所属的文档， $n_m^{(k)}$ 是主题 $k$ 在文章 $m$ 中出现的次数。对 $\Theta$ 积分可得：

\[\begin{align} p(\z|\a) &= \int p(\z|\Theta)p(\Theta|\a)\mathrm{d}\Theta \\ &= \int \prod_{m=1}^M {1 \over \Delta(\a)} \prod_{k=1}^K \vartheta_{m,k}^{n_m^{(k)}+\alpha_k-1} \mathrm{d}\vt_m \\ &= \prod_{m=1}^M {\Delta(\vec{n}_m + \a) \over \Delta(\a)}, \quad \vec{n}_m = \brace{n_m^{(k)}}_{k=1}^K \end{align}\]

由如上两部分得到联合分布：

\[p(\z,\w|\a,\b) = \prod_{z=1}^K {\Delta(\vec{n}_z+\b) \over \Delta(\b)} \cdot \prod_{m=1}^M {\Delta(\vec{n}_m+\a) \over \Delta(\a)}\]

根据联合分布，求解下标为 $i=(m,n)$ 的词，即第 $m$ 篇文档中的第 $n$ 个词，的全部的条件概率。令 $\w = \brace{w_i=t, \w_{\neg{i}}}$ ， $\z = \brace{z_i=k, \z_{\neg{i}}}$ ，有：

\[\begin{align} p(z_i=k|\z_{\neg{i}},\w) &= {p(\w,\z) \over p(\w,\z_{\neg{i}})} \\ &= {p(\w,\z) \over p(\w_{\neg{i}}|\z_{\neg{i}}) p(w_i)} \cdot {p(\z) \over p(\z_{\neg{i}})} \\ &\propto {\Delta(\vec{n}_z+\b) \over \Delta(\vec{n}_{z,\neg{i}} +\b)} \cdot {\Delta(\vec{n}_m+\a) \over \Delta(\vec{n}_{m,\neg{i}} +\a)} \\ &= {\Gamma(n_k^{(t)}+\beta_t)\Gamma(\sum_{t=1}^V n_{k,\neg{i}}^{(t)}+\beta_t) \over \Gamma(n_{k,\neg{i}}^{(t)}+\beta_t)\Gamma(\sum_{t=1}^V n_k^{(t)}+\beta_t)} \cdot {\Gamma(n_m^{(k)}+\alpha_k)\Gamma(\sum_{k=1}^K n_{m,\neg{i}}^{(k)}+\alpha_t) \over \Gamma(n_{m,\neg{i}}^{(k)}+\alpha_t)\Gamma(\sum_{k=1}^K n_m^{(k)}+\alpha_k)} \\ &= {n_{k,\neg{i}}^{(t)} +\beta_t \over \sum_{t=1}^V n_{k,\neg{i}}^{(t)} +\beta_t} \cdot {n_{m,\neg{i}}^{(k)} +\alpha_k \over [\sum_{k=1}^K n_m^{(k)} +\alpha_k] -1} \\ &\propto {n_{k,\neg{i}}^{(t)} +\beta_t \over \sum_{t=1}^V n_{k,\neg{i}}^{(t)} +\beta_t} (n_{m,\neg{i}}^{(k)}+\alpha_k) \tag 8 \end{align}\]

最终，我们需要根据Markov链的状态 $z_i$ 获取多项分布的参数 $\Theta$ 和 $\Phi$ 。根据贝叶斯法则和Dirichlet先验，以及公式(6)和(7)：

\[\begin{align} p(\vt_m|\z_m,\a) &= {1 \over Z_{\vartheta_m}} \prod_{n=1}^{N_m}p(z_{m,n}|\vt_m) \cdot p(\vt_m|\a) = \mathrm{Dir}(\vt_m|\vec{n}_m+\a) \\ p(\vp_k|\z,\w,\b) &= {1 \over Z_{\varphi_k}} \prod_{\brace{i:z_i=k}}p(w_i|\vp_k) \cdot p(\vp_k|\b) = \mathrm{Dir}(\vp_k|\vec{n}_k+\b) \end{align}\]

其中， $\vec{n}_m$ 是构成文档 $m$ 的主题数向量， $\vec{n}_k$ 是构成主题 $k$ 的词项数向量。求解Dirichlet分布的期望，即公式(4)可得：

\[\begin{align} \varphi_{k,t} &= {n_k^{(t)}+\beta_t \over \sum_{t=1}^V n_k^{(t)} +\beta_t} \tag 9 \\ \vartheta_{m,k} &= {n_m^{(k)}+\alpha_k \over \sum_{k=1}^K n_m^{(k)} +\alpha_k} \tag {10} \end{align}\]

梳理一下Gibbs sampling中所用到的数据结构：统计量 $n_m^{(z)}$ 和 $n_z^{(t)}$ 分别是 $M \times K$ 和 $K \times V$ 矩阵，它们每行的和分别是 $M$ 维向量 $n_m$ (文档长度)和 $K$ 维向量 $n_z$ 。Gibbs sampling算法有三个阶段：初始化、burn-in和sampling。具体算法如下：

• 算法： $\mathrm{LdaGibbs}(\brace{\w,\alpha,\beta,K})$
• 输入：单词向量 $\w$ ，超参数 $\alpha$ 和 $\beta$ ，主题数 $K$
• 全局变量：统计量 $\brace{n_m^{(k)}}$ 、 $\brace{n_k^{(t)}}$ ，以及它们的总数 $\brace{n_m}$ 、 $\brace{n_k}$ ，全部条件概率数组 $p(z_i\vert\cdot)$
• 输出：主题向量 $\brace{\z}$ ，多项分布参数 $\Phi$ 和 $\Theta$ ，超参数估计量 $\alpha$ 和 $\beta$

[初始化]

• 设置全局变量 $n_m^{(k)}$ 、 $n_k^{(t)}$ 、 $n_m$ 、 $n_k$ 为零
• 对所有文档 $m \in [1, M]$ ：
  • 对文档 $m$ 中的所有单词 $n \in [1, N_m]$ ：
    • 初始化每个单词对应的主题 $z_{m,n}=k \sim \mathrm{Mult}(1/K)$
    • 增加“文档-主题”计数： $n_m^{(k)}+=1$
    • 增加“文档-主题”总数： $n_m +=1$
    • 增加“主题-词项”计数： $n_k^{(t)}+=1$
    • 增加“主题-词项”总数： $n_k +=1$

[迭代下面的步骤，直到Markov链收敛]

• 对所有文档 $m \in [1, M]$ ：
  • 对文档 $m$ 中的所有单词 $n \in [1, N_m]$ ：
    • 删除该单词的主题计数： $n_m^{(k)}-=1; n_m-=1; n_k^{(t)}-=1; n_k-=1;$
    • 根据公式(8)采样出该单词的新主题： $\tilde{k} \sim p(z_i\vert\z_{\neg{i}}, \w)$
    • 增加该单词的新主题计数： $n_m^{(\tilde{k})}+=1; n_m+=1; n_\tilde{k}^{(t)}+=1; n_\tilde{k}+=1;$
• 如果Markov链收敛：
  • 根据公式(9)生成主题-词项分布 $\Phi$
  • 根据公式(10)生成文档-主题分布 $\Theta$

参考

• Gregor Heinrich, Parameter estimation for text analysis
• David M.Blei, Andrew Y.Ng, Michael I.Jordan, Latent Dirichlet Allocation
• Philip Resnik, Eric Hardisty, Gibbs Sampling for the Uninitiated