《统计自然语言处理》笔记

Posted on |

《统计自然语言处理》第二版，宗成庆

1 绪论

1.2.1 自然语言处理研究的内容

  • 机器翻译（machine translation, MT）
  • 自动文摘（automatic summarizing / abstracting）
  • 信息检索（information retrieval）
  • 文档分类（document / text categorization / classification）
  • 问答系统（question-answering system）
  • 信息过滤（information filtering）
  • 信息抽取（information extraction）
  • 文本挖掘（text/data mining）
    • 文本分类（text classification）
    • 文本聚类（text clustering）
    • 实体抽取（concept / entity extraction）
    • 粒度分类
    • 情感分析（sentiment analysis）
    • 自动文摘
    • 实体关系建模（entity relation modeling）
  • 舆情分析（public opinion analysis）
  • 隐喻计算（metaphorical computation）
  • 文字编辑和自动校对（automatic proofreading）
  • 作文自动评分
  • 光读字符识别（optical character recognition, OCR）
  • 语音识别（speech recognition, ASR）
  • 文语转换（text-to-speech conversion）
  • 说话人识别（speaker recognition / identification / verification）

1.2.3 自然语言处理面临的困难

开塔兰数（Catalan numbers，$C_n$），歧义组合的复杂程度随着介词短语个数的增加而不断加深，如果句子中存在n个介词短语，则 $C_n = {2n \choose n} {1 \over n+1}$。

1.3.1 自然语言处理的基本方法

  • 理性主义（rationalist）乔姆斯基（Noam Chomsky）符号处理系统 -> 试图刻画人类思维模式
  • 经验主义（empiricist）统计自然语言处理 -> 关注真实的语言本身

2 预备知识

2.2.6 困惑度（perplexity）

语言 $L=(X_i)~p(x)$ 与模型 $q$ 的交叉熵

\[H(L,q)=-\lim_{n\to\infty}\frac1n\sum_{x_1^n}p(x_1^n)\log q(x_1^n)\]

评估语言模型一般用困惑度（交叉熵在指数位置）

\[PP_q=2^{H(L,q)} \approx 2^{-\frac1n\log q(l_1^n)} = [q(l_1^n)]^{-\frac1n}\]

4 语料库与语言知识库

北京大学综合型语言知识库

北京大学计算语言学研究所（ICL/PKU） 综合型语言知识库（CLKB）俞士汶

4.2.5 知网（HowNet）

义原
最基本的、不易于再分割其意义的最小单位。

4.3 语言知识库与本体论（ontology）

希腊文onto = 英文being

本体的核心概念是知识共享，通过减少概念和术语上的歧义，建立一个统一的框架或规范模型，使得来自不同背景、持不同观点和目的的人员之间理解和交流，以及不同系统之间的互操作或数据传输成为可能，并保持语义上的一致。

5 语言模型

5.1 n元语法

基元
可以是字、词或短语，一般指词。
语言模型（Language Model）
通常构建为字符串s的概率分布$p(s)$，这里$p(s)$试图反应的是字符串s作为一个句子出现的频率。
\[\begin{align} p(s) &= p(w_1)p(w_2|w_1)\cdots p(w_l|w_1\cdots w_{l-1}) \\ &= \prod_{i=1}^l p(w_i|w_1\cdots w_{i-1}) \end{align}\]

bigram，二元文法模型，一阶马尔可夫链（Markov chain）

\[\begin{align} p(s) &= \prod_{i=1}^l p(w_i |w_i\cdots w_{i-1}) \\ & \approx \prod_{i=1}^l p(w_i |w_{i-1}) \end{align}\]

用于构建语言模型的文本称为训练语料（training corpus），估计$p(w_i\vert w_{i-1})$一般用MLE。

为啥要平滑算法？

6 概率图模型

常见图模型的分类关系

PGM

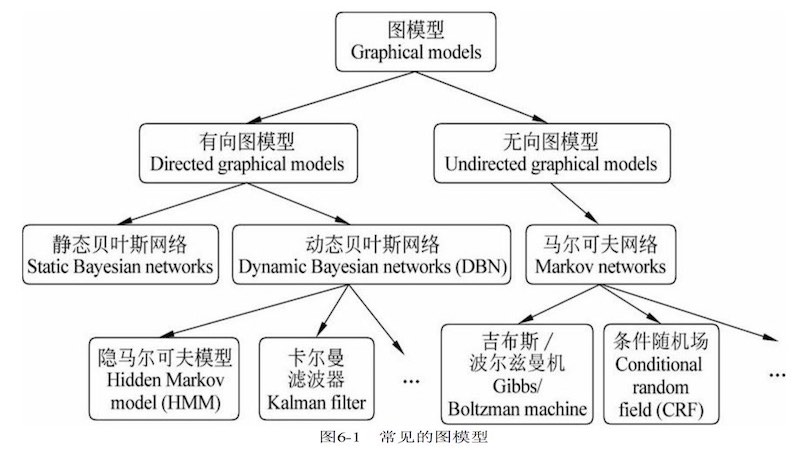
  • 横向：点 -> 线 -> 面
  • 纵向：生成式 p(x,y) -> 判别式 p(y\vert x)
生成模型(generative) 判别模型(discriminative)
因果性 相关性
联合概率 $p(x,y)$ 条件概率 $p(y\vert x)$
概率图是有向图 概率图是无向图
需要每类别的具体分布，无限样本 只需要关注类别边界，有限样本
例如：Bayes、HMM、LDA 例如：LR、SVM、NN、CRF

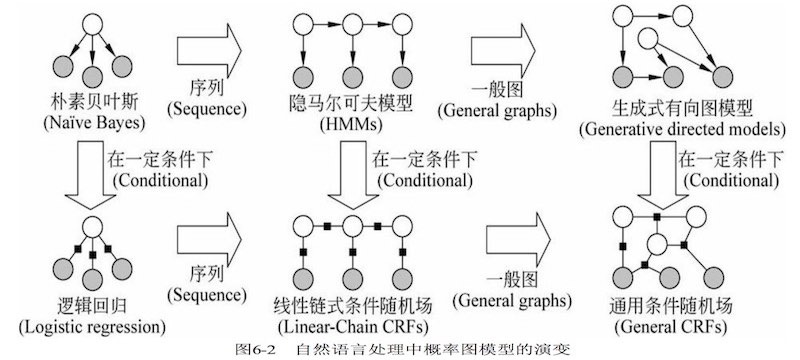
PGM Evolution

6.2 贝叶斯网络

贝叶斯网络 -> DAG

  • 结点：随机变量，可以是可观测量、隐含变量、未知参数或假设等。
  • 有向边：条件依存关系，如果两点之间无边则表示该两变量在某些特定情况下条件独立。

每个结点都与一个概率函数有关，概率函数的输入是该结点的父结点所表示随机变量的一组特定值，输出为当前结点表示随机变量的概率值。

假设父结点有n个随机变量，概率函数可表示为由$2^n$个条目组成的二维表。

比如，事件H, S, N，如果S依赖N，而H依赖S, N（即S父结点是N，H父结点是S和N）， 则事件H的概率可表示为P(H|S, N)，三者的联合概率：P(H, S, N) = P(H|S, N) * P(S|N) * P(N)。

构造贝叶斯网络是个复杂的任务，涉及表示、推断、学习三个方面的问题：

  • 表示：即使随机变量只有两种取值，一个联合概率也有 2n 种概率值
  • 推断：变量消除法、团树法；近似推理：重要性抽样、MCMC、循环信念传播
  • 学习：MLE、MAP、EM、贝叶斯估计

6.3 马尔可夫模型

马尔可夫模型（Markov Model）描述一类重要的随机过程。

研究的问题：一个随机变量序列，且随机变量并不是互相独立，每个随机变量的值依赖于序列前面的状态。

两个基本概念：

  • 系统有$N$个有限状态 $S=\brace{s_1,s_2,\cdots,s_N} $
  • 随机变量序列 $Q=\brace{q_1,q_2,\cdots,q_t,\cdots,q_T} $，其中 $q_t \in S$

系统在时间 $t$ 处于状态 $s_i$ 的概率取决于其在时间 $1,2,\cdots,t-1$ 的状态。如果只依赖于时间 $t-1$ 的状态，则是马尔科夫链（Markov Chain）：

\[P(q_t=s_i|q_{t-1}=s_j,q_{t-2}=s_k,\cdots) = P(q_t=s_i|q_{t-1}=s_j)\]

【注】这个公式书里感觉搞错下标了。

上式独立于时间$t$的随机过程，即为马尔可夫模型：

\[P(q_t=s_j|q_{t-1}=s_i) = a_{ij}, \qquad 1\leq i,j\leq N\]

核心是转移概率 $a_{ij}$ 可以组成一个转移概率矩阵，且满足约束：$a_{ij} \geq 0, \quad \sum_{j=1}^N a_{ij} = 1$。

马尔可夫模型下所有变量的联合概率：

\[\begin{align} P(q_1,q_2,\cdots,q_T) &= P(q_1)P(q_2|q_1)P(q_3|q_1,q_2)\cdots P(q_T|q_1,q_2,\cdots,q_{T-1}) \\ &= P(q_1)P(q_2|q_1)P(q_3|q_2)\cdots P(q_T|q_{T-1}) \\ &=\pi_{q_1} \prod_{t=1}^{T-1} a_{q_t q_{t+1}} \end{align}\]

其中，$\pi_{q_1}=P({q_1})$ 是初始概率。

马尔可夫模型又可视为随机的有限状态机。

6.4 隐马尔可夫模型

区别于MM，HMM不知道随机变量序列所对应的状态，能观察到的是该状态的概率函数，因此HMM是一个双重的随机过程。理解的关键是观察概率图的箭头方向。

HMM

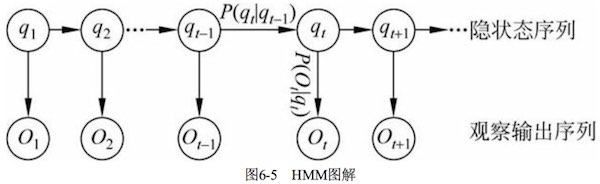
可以看到HMM有两组变量序列，所以对比MM的有限状态集合$S$，还多了一个输出符号集合$V$。

  • 隐状态序列 $\brace{q_1,q_2,\cdots,q_t,\cdots} $，其中，$t$时刻系统状态$q_t \in S$，是隐变量。
  • 观察输出序列 $\brace{ O_1,O_2,\cdots,O_{t},\cdots} $，其中 $t$时刻系统输出符号$O_t \in V$，是能观察到的值。

所以，HMM五元组 $\mu=(S, V, A, B, \pi)$

  • S: 有限状态的集合 $S=\brace{ s_1,s_2,\cdots,s_N} $
  • V: 输出符号的集合 $V=\brace{ v_1,v_2,\cdots,v_K} $
  • A: 状态转移概率矩阵 \(\brace{ a_{ij}}_{N\times N}\)，其中 \(a_{ij}=P(q_{t+1}=s_j\vert q_t=s_i)\)
  • B: 符号发射概率矩阵 \(\brace{ b_{ij}}_{K\times K}\)，其中 \(b_{ij}=P(O_t=v_j\vert q_t=s_i)\)
  • π: 初始状态的概率分布 $\brace{ \pi_1,\cdots,\pi_N} $，其中 $\pi_i=P(q_1=s_i)$

【注】书输出符号集用的K，但输出符号步骤又用了v，我这边修正了符号。

同样，应该能够写出HMM下所有变量的联合概率：

\[\begin{align} P(q_1,O_1,q_2,O_2,\cdots,q_T,O_T) &= P(q_1,O_1)P(q_2,O_2|q_1)\cdots P(q_T,O_T|q_{T-1}) \\ &= P(q_1)P(O_1|q_1)P(q_2|q_1)P(O_2|q_2)\cdots P(q_T|q_{T-1})P(O_T|q_T) \\ &=\pi_{q_1} \prod_{t=1}^{T-1} a_{q_t q_{t+1}} b_{q_t O_t} \end{align}\]

假设给定模型 $\mu=(A, B, \pi)$，则观察输出序列 $O=O_1O_2\cdots O_t$ 可以由如下步骤产生：

  1. 根据初始状态的概率分布 $\pi_i$ 选择一个初始状态 $q_1=s_i$;
  2. 设 $t=1$;
  3. 根据状态 $s_i$ 的输出概率分布 $b_i(k)$ 输出 $Q_t=v_k$;
  4. 根据状态转移概率分布 $a_{ij}$，将当前时刻$t$的状态转移到新状态 $q_{t+1}=s_j$;
  5. $t=t+1$，如果 $t<T$，重复步骤(3)和(4)，否则结束算法。

HMM的三个基本问题：

  • 估计问题：给定观察序列 $O$ 和模型 $\mu$，求解 $O$ 的概率 $P(O\vert \mu)$。前向算法、后向算法。
  • 序列问题：给定观察序列 $O$ 和模型 $\mu$，寻找最优状态序列 $Q$，求解$\arg\max_Q P(Q\vert O,\mu)$。Viterbi算法。
  • 参数估计问题：给定观察序列 $O$，MLE求解 $\arg\max_\mu P(O\vert \mu)$。前向后向算法。

动态规划方法。

6.7 最大熵模型

6.7.1 最大熵原理

最大熵原理
在已知部分信息的前提下，关于某未知分布最合理的推断应该是选择熵最大的推断。

两个主要概念：特征函数、约束条件。

符号说明，比如词性标注问题：

  • A 待消歧问题所有可能候选结果的集合。如：动词、名词、形容词
  • B 当前歧义点所在上下文信息构成的集合。如：某个词和它的上下文。
  • f(a,b) 定义在$\brace{0,1} $域上的二值函数，即特征函数。如：a:动词；b: 动词+“阅读”+名词；f(a,b)=1，判断“阅读”是动词为真。

应用最大熵原理，选择条件概率 $p(a\vert b)$ 熵最大的候选结果作为最终的判定结果（目标函数）：

\[\begin{align} p(a|b) &= \arg\max_{p\in P} H(p) \\ &= \arg\max_{p\in P} -\sum_{a,b} p(b)p(a|b)\log p(a|b) \end{align}\]

其中，$P$是满足条件的概率分布集合，也就是这个最优化问题的约束条件。

设置约束条件的主要思路：模型的概率分布应该与训练样本的一致。

已知经验分布 $\hat{p}(a,b) \approx {\mathrm{Count}(a,b) \over \sum_{A,B}\mathrm{Count}(a,b)}$ ，可知特征函数 $f_i(a,b)$ 在训练样本中关于经验分布 $\hat{p}(a,b)$ 的期望：

\[E_{\hat p}(f_i) = \sum_{A,B}\hat{p}(a,b) f_i(a,b)\]

而特征函数 $f_i(a,b)$ 在理论模型 $p(a,b)$ 的期望是：

\[\begin{align} E_p(f_i) &= \sum_{A,B}p(a,b) f_i(a,b) \\ &= \sum_{A,B} p(b) p(a|b) f_i(a,b) \\ &= \sum_{A,B} \hat{p}(b) p(a|b) f_i(a,b) \end{align}\]

【注】书里公式6-36用 $p(a\vert b)=p(a)p(b\vert a)$ 替换感觉不对啊，要约束的对象不是 $p(a\vert b)$ 吗？

这就构成了一系列约束条件（共有$k$个特征函数）：

\[P = \{ p(a|b) | E_p(f_i)=E_\hat{p} (f_i), \quad i\in \{1,2,\cdots,k\} \}\]

对这样带约束的最优化问题，使用拉格朗日乘子法求解，可得：

\[\hat{p}(a|b) = {\exp\left( \sum_{i=1}^{k+1} \lambda_i f_i(a,b) \right) \over \sum_A \exp\left( \sum_{i=1}^{k+1} \lambda_i f_i(a,b) \right) }\]

其中，$\lambda_i$ 是特征 $f_i$ 的权重。

6.8 最大熵马尔可夫模型

MEMM广泛应用于序列标注问题。

6.9 条件随机场

CRF可以看作一个无向图模型或马尔可夫随机场。

7 自动分词、NER与词性标注

从计算的严格意义上说，自动分词是一个没有明确定义的问题 [黄昌宁等, 2003]。 原因：单字词vs语素、词vs短语(词组) 之间的界限不明确。

歧义：

  • 交集型，偶发歧义。AJB，满足AJ、JB同时为词。如：大学生、研究生物、为人民工作、中国产品质量
  • 组合型，固有歧义。AB，满足A、B、AB同时为词。如：起身、将来、现在、才能、学生会

未登录词：

  • 新出现的普通词汇，如网络词汇
  • 专有名词：命名实体（Named Entity），造成分词错误的主要原因
    • 人名
    • 地名
    • 组织机构名
  • 专业名词和研究领域名称
  • 其他专用名词，如新出现的产品名，电影、书籍等作品名。

7.2 汉语分词方法

两个主要问题：切分歧义消除、未登录词识别。

7.3 命名实体识别

实体概念在文本中的引用（Entity Mention）有三种形式：

  • 命名性指称。如，刘国梁
  • 名词性指称。如，中国乒乓球队主教练
  • 代词性指称。如，他

基于统计模型的NER方法有很多种：

  • 有监督：HMM、n-gram、ME、SVM、CRF等
  • 半监督：自举学习
  • 无监督：利用词汇资源进行上下文聚类
  • 混合型

7.3.2 基于CRF的命名实体识别方法

类似汉语分词原理，把NER看成一个序列标注问题：

  1. 分词；
  2. 识别人名、简单地名、简单组织名；
  3. 识别复合地名、符合组织名。

有监督学习，需要已标注的大规模语料，常用 北京大学计算语言学研究所 标注的现代汉语多级加工语料库。

步骤：标注语料 -> 产生特征 -> 训练模型 （比一般ML过程多一步标注语料）

7.5 词性标注

词性（pos, part-of-speech）是词汇最基本的语法属性，也称作词类。

7.7 技术评测

分词、NER、词性标注，这三者是中文信息处理的基础性关键技术。

分词：F1 NER：MUC-6会议

11 统计机器翻译

11.2 基于噪声信道模型的统计机器翻译原理

由IBM研究人员提出：一个翻译系统看成一个噪声信道，对于一个观察到的信道输出 $S$，寻找最大可能的输入 $T$，求解 $\arg\max_T P(T\vert S)$，根据贝叶斯公式即求解 $\arg\max_T P(T)P(S\vert T)$。

概率 $P(T)$ 为目标语言的语言模型，$P(S\vert T)$ 给定T情况下 $S$ 的翻译概率，称作 翻译模型。

统计翻译就是根据信道输出搜索最大可能的信道输入过程，即噪声信道模型中的解码过程。因此，这个搜索过程的模块称作 decoder。

SMT

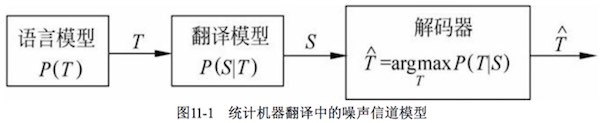
T和S的词之间存在 对齐（alignment）问题，刻画这种对齐关系的模型称作alignment model。

14 信息检索与问答系统

标引（indexing）：query和候选doc，表示为词向量； 相关性计算（similarity/relevance）：计算query和候选doc之间的相关性。

存在问题：一词多义（polysemy）、一义多词（synonymy）。

14.1.2 基本方法和模型

布尔模型、VSM、概率模型、语言模型

14.2 隐含语义标引模型

LSI建立query和doc之间的语义联系。