[TOC]
决策树是一种很常用分类学习算法,它的学习结果非常易于理解和解释,就是一组用于划分假设空间的if-else规则的集合。决策树由结点和边组成。结点有两种类型:内部结点,表示一个特征或属性;叶结点,表示一个类别。边表示相应结点对应特征的取值。
决策树学习算法包含特征选择、树的生成和树的剪枝三个过程。决策树表示给定特征条件下类的条件概率分布,决策树的深浅对应着不同复杂度的概率模型。决策树根据不同特征对训练集的划分递归生成,对应于模型的局部选择,树的生成只考虑局部最优。决策树的剪枝则是为了避免决策树过拟合,提高决策树的泛化能力,树的剪枝考虑全局最优。
特征选择
信息增益
信息增益(information gain)在前文已有叙述。简单说就是,特征 $T$ 给系统带来的信息增益是系统原本的熵与固定特征 $T$ 后的条件熵之差。
\[g(T,C) = H(C) - H(C|T)\]具体的特征选择方法是:对训练集数据计算每个特征的信息增益,选择信息增益最大的那个特征。
由于信息增益的大小是相对训练集而已,并无绝对意义。因此,在ID3中用信息增益选择属性时,总是偏向于选择分枝比较多的属性值,即取值多的属性。Quinlan后来在C4.5中对此做了改进,使用增益率(gain ratio),即把信息增益除以 $H(C)$ 。
\[g_R(T,C) = \frac{g(T,C)}{H(C)}\]树的生成
ID3本质是贪心算法,递归的在每个结点处选择“最佳特征”来划分决策空间,自顶向下构建出决策树。算法如下:
Function ID3(R: 待训练的所有特征集合,
C: 待分类的类别属性集合,
S: 训练集) 返回一颗决策树
Begin
If S均属于相同类别, Return 该类别叶节点
If R为空, Return S中出现频率最高的类别叶节点
设 D 是 R 中拥有最大信息增益 g(D,S) 的特征
设 {dj|j=1,...,m} 是特征 D 的所有取值集合
设 {Sj|j=1,...,m} 是固定特征值 dj 后得到的 S 的所有子集
返回一棵树, 其根标记为 D, 树枝标记为 d1,...,dm
递归求解 ID3(R-D, C, S1),.., ID3(R-D, C, Sm) 其中 R-D 表示从特征属性集合 R 中刨除掉已选择特征 D
End ID3
下面利用ID3算法来做点具体的事情,采用Michell的打网球的示例数据,需要根据天气状况预测是否打网球:
Outlook Temperature Humidity Wind PlayTennis
Sunny Hot High Weak No
Sunny Hot High Strong No
Overcast Hot High Weak Yes
Rain Mild High Weak Yes
Rain Cool Normal Weak Yes
Rain Cool Normal Strong No
Overcast Cool Normal Strong Yes
Sunny Mild High Weak No
Sunny Cool Normal Weak Yes
Rain Mild Normal Weak Yes
Sunny Mild Normal Strong Yes
Overcast Mild High Strong Yes
Overcast Hot Normal Weak Yes
Rain Mild High Strong No
数据的第一行是特征名,前面几列都是具体特征值,最后一列是需要分类的类别值。Python示例代码如下:
#!/usr/bin/env python
# -*- coding: utf-8; tab-width: 4; -*-
#
import collections
import math
class DecisionTreeId3(object):
'''ID3分类决策树demo,仅接收离散特征'''
def __init__(self, data, featureNameList, targetName):
'''data 训练数据集 list of dict结构
featureNameList 特征列名列表
targetName 类别列明'''
self.data = data
self.featureNameList = featureNameList
self.targetName = targetName
# 生成的决策树,类似 ('feat1', {1: ('feat2', ..), {2: ..}, ..}) 的结构
self.tree = None
def _entropy(self, data):
'''计算信息熵'''
frequency = collections.defaultdict(lambda: 0.0)
entropy = 0.0
for row in data:
frequency[row[self.targetName]] += 1
for freq in frequency.values():
entropy += (-freq/len(data)) * math.log(freq/len(data))
return entropy
def _cond_entropy(self, data, featureName):
'''计算某特征的条件熵'''
frequency = collections.defaultdict(lambda: 0.0)
entropy = 0.0
for row in data:
frequency[row[featureName]] += 1
for val, freq in frequency.items():
prob = freq/len(data)
d = [row for row in data if row[featureName] == val]
entropy += prob * self._entropy(d)
return entropy
def _entropy_gain(self, data, featureName):
'''如果是C4.5则改用信息增益率'''
return self._entropy(data) - self._cond_entropy(data, featureName)
def _one_target(self, data):
'''判断数据集中是否只有一个类别'''
return len(set([row[self.targetName] for row in data])) <= 1
def _major_target(self, data):
'''获取数据集中最多的类别'''
frequency = collections.defaultdict(lambda: 0.0)
for row in data:
frequency[row[self.targetName]] += 1
majorTarget = None
majorTargetFreq = 0
for targetValue, freq in frequency.items():
if freq > majorTargetFreq:
majorTargetFreq = freq
majorTarget = targetValue
return majorTarget
def _subset_data(self, data, featureName, featureValue):
'''根据某特征的取值划分数据集'''
newData = []
for row in data:
if row[featureName] == featureValue:
newRow = row.copy()
del(newRow[featureName])
newData.append(newRow)
return newData
def _make_tree(self, data, featureNameList):
'''按照ID3算法创建决策树'''
if self._one_target(data):
return data[0][self.targetName]
elif not featureNameList:
return self._major_target(data)
else:
splitFeat = None
maxGain = 0
for feat in featureNameList:
gain = self._entropy_gain(data, feat)
if gain > maxGain:
maxGain = gain
splitFeat = feat
tree = (splitFeat, {})
for val in set(row[splitFeat] for row in data):
newData = self._subset_data(data, splitFeat, val)
newFeatNameList = [f for f in featureNameList if f != splitFeat]
subtree = self._make_tree(newData, newFeatNameList)
tree[1][val] = subtree
return tree
def train(self):
self.tree = self._make_tree(self.data, self.featureNameList)
def _search_tree(self, tree, row):
if isinstance(tree, basestring):
return tree
featureName = tree[0]
subtree = tree[1][row[featureName]]
return self._search_tree(subtree, row)
def predict(self, row):
if not self.tree: self.train()
return self._search_tree(self.tree, row)
def main():
import sys
features = []
data = []
for line in sys.stdin:
if not features:
features = line.strip().split()
else:
data.append(dict(zip(features, line.strip().split())))
foldNum = int(0.2 * len(data))
dt = DecisionTreeId3(data[:-foldNum], features[:-1], features[-1])
dt.train()
for row in data[-foldNum:]:
c = row[features[-1]]
del(row[features[-1]])
print c, dt.predict(row)
if __name__ == "__main__":
main()
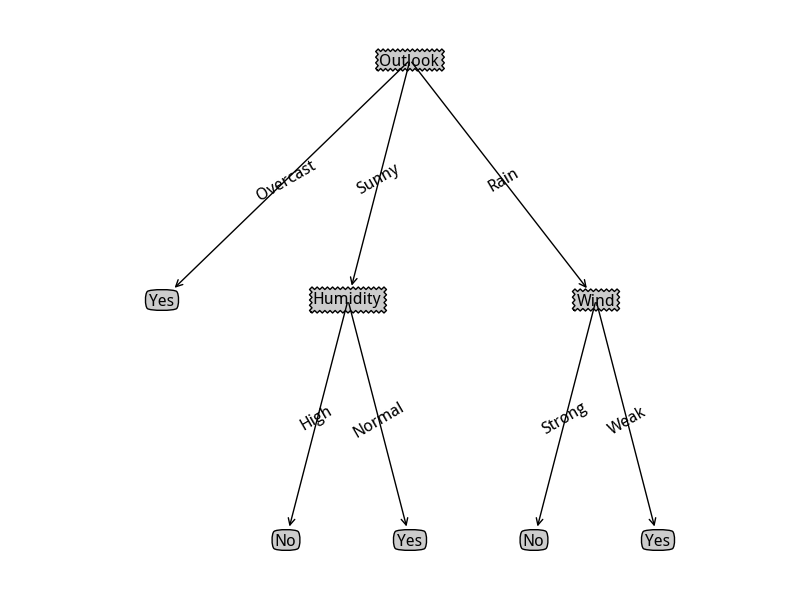
利用这个绘图脚本,可以输出决策树的直观图示:
C4.5
C4.5除了使用增益率来做特征选择外,还可以处理连续特征。
因为虽然特征的属性值是连续的,但对于有限的采样数据是离散的。假定N份训练样本,则其中某连续特征最多有N个取值,那么该特征就有N-1个划分点,取其中信息增益最大的划分,即是要找的划分阈值,这样可以把连续特征转换成离散特征来处理。
对连续属性值的划分可以进一步优化,先对属性值排序,只有在类别发生变化的地方进行划分,这样可以显著减少划分次数。
树的剪枝
在实际构造决策树时,通常要进行剪枝,这是为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种:
- 先剪枝:在构造过程中,当某个节点满足剪枝条件,则直接停止此分支的构造。
- 后剪枝:先构造完成完整的决策树,再通过某些条件遍历树进行剪枝。
MDL
归纳偏置(Inductive Bias)
奥卡姆剃刀
参考
- 数据挖掘导论 Pan-Ning Tan 4.3.决策树归纳
- 机器学习 Michell 3.决策树学习
- Building Classification Models: ID3 and C4.5