前面的章节属于概率论,从第四章开始属于数理统计学(Statistics)。 概率论更偏纯数学,包括随机变量、概率、随机、方差、大数定理等,从三条公理出发,所有的定理都有严格证明推导; 而统计学更偏应用,包括参数估计、假设检验、方差分析、统计推断等。
统计学是这样一门学科: 它使用概率论和数学的方法,研究怎样收集(通过实验或观察)带有随机误差的数据,并在设定的模型(称作统计模型)之下,对这种数据进行分析(称作统计分析),以对所研究的问题作出推断(称作统计推断)。
统计学的两个重要问题:
- 参数估计,计算数据分布的参数值
- 假设检验
[TOC]
第四章 参数统计
4.1.1 总体
总体:与所研究问题有关的对象的全体构成的集合。
无限总体 (Fisher提出)
比如,某物体的真实重量α未知,要通过多次测量估计它。总体是一切可能的测量结果,此时即称为无限总体。该总体符合某某分布。
样本:按一定规定从总体里抽样出的一部分个体。
放回抽样 和 不放回抽样
在有限总体的情况下是有区别的,此时样本分布和总体分布可能会不一致,抽样方式也要作为一个要素放入统计模型; 但在无限总体下,总体分布完全决定了样本分布,故可以把总体分布等同于统计模型。
自助抽样(Bootstrap)
4.1.4 统计量(Statistical parameter / Population parameter)
完全由样本决定的量,称为统计量。
【注】统计量只能依赖于样本,而不能依赖任何其它未知的量。特别的是,不能依赖于总体分布中所包含的未知参数。
有用的统计量:样本均值、样本方差、样本矩。
k阶样本原点矩:
\[a_k = {X_1^k+\dots+X_n^k \over n}\]k阶样本中心矩:
\[m_k={\sum_{i=1}^n X_i - \bar{X} \over n }\]1阶样本原点矩即样本均值。
2阶样本中心距和样本方差相差n/(n-1)。
【注】为什么样本方差需要除以n-1而不是n?(和自由度有关,详见4.3节 例3.2)
4.2 矩估计、极大似然估计和贝叶斯估计
总体分布的概率密度函数(pdf),记作:f(x; θ),其中,θ是该分布的未知参数。
4.2.3 极大似然估计
对 f(x; θ),如果固定x,把θ看做变量,记作 L(x; θ)。这里θ有一定的值(虽然未知),并非事件或随机变量,无概率可言,所以改称作“似然”。L(x; θ)即为似然函数。用似然程度最大的θ’去作为真实θ的估计值(因为此时在已知样本x条件下,似然程度最大的θ’最接近真实θ),即为最大似然估计。
\[\log L = \sum_{i=1}^n \log f(x; \theta)\]为了使L最大,若f对θ存在连续偏导时,则取偏导为0的点。即求解如下方程组:
\[{\partial \log L \over \partial \theta_i} = 0, \qquad i=1,\dots,k\]4.2.4 贝叶斯估计
区别在于对参数θ的处理:
- 矩估计、最大似然估计:参数θ只是简单一个未知数,在抽取样本之前,我们对θ没有任何了解,所有的信息都来自样本;
- 贝叶斯估计:在抽样之前,我们对θ已经有了先验知识,即θ也是一个随机变量,符合某种概率分布,称作θ的先验分布,先验密度函数记作h(θ)。
4.3 点估计的优良性准则
估计量的无偏性: 1) 没有系统性偏差 bias? 2) 由大数定理,估计值的均值无限逼近真值。
【注】为什么方差$S^2$需要除以$n-1$的一种解释: $\sum_{i=1}^n (X_i-\bar{X})^2 $ 自由度为$n-1$。 因为一共$n$个样本有$n$个自由度,用样本方差$S^2$去估计总体方差$\sigma^2$,自由度本来应该是$n$,但由于总体均值$\alpha$也未知,用${\bar X}$去估计,这就用掉了一个自由度,于是只剩下$n-1$个自由度。 如果总体均值$\alpha$已知,则不用$S^2$去估计$\sigma^2$,而使用 $\sum_{i=1}^n(X_i-\alpha)^2/n$ 去估计,此时分母为$n$,这是$\sigma^2$的无偏估计。
4.3.2 最小方差无偏估计
均方误差(Mean Squared Error, MSE)
4.3.3 估计量的相合性和渐进正态性
4.4 区间估计(Interval estimate)
目标:估计参数 θ 落在区间 [θ1, θ2] 的概率 P(θ1≤θ≤θ2),应该尽量让区间小(精确度),且概率高(可靠性)。其中,[θ1, θ2] 即为置信区间(Confidence interval)。
【定义】给定一个很小的数 α>0,如果对于参数θ的任何值,概率 P(θ1≤θ≤θ2) ≥ 1-α,则称 1-α 为置信区间[θ1, θ2]的 置信系数(Confidence level / Confidence coefficient)。
4.4.2 枢轴变量法
示例,设X是抽自正态总体$N(\mu,\sigma^2)$的样本,方差$\sigma^2$已知,要求均值$\mu$的区间估计。
先寻找$\mu$的无偏点估计,如样本均值$\bar{X}$,由样本总体为正态分布,可知(即枢轴变量):
\[\sqrt{n}{\bar{X}-\mu \over \sigma} \sim N(0,1)\]以$\phi$记作N(0,1)的分布函数,对 0<β<1(一般β很小),用方程 $\phi(u_\beta)=1-\beta$,定义记号$u_\beta$。
则$u_\beta$称为分布N(0,1)的 “上β分位点”。其意义是N(0,1)分布中大于$u_\beta$那部分的概率(积分),即β(面积)。
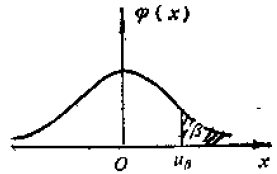
传统上,这个分位点都可以查表获得。
注意分布的两侧都有分位点,所以其实$\beta = {\alpha \over 2}$:
\[P\left(-u_{\alpha \over 2} \leq \sqrt{n}{\bar{X}-\mu \over \sigma} \leq u_{\alpha \over 2} \right) = \phi(u_{\alpha \over 2}) - \phi(-u_{\alpha \over 2}) = 1-\alpha\]变换一下:
\[P\left({\bar{X} - \sigma u_{\alpha \over 2} \over \sqrt{n}} \leq \mu \leq {\bar{X}+\sigma u_{\alpha \over 2} \over \sqrt{n}} \right) = 1- \alpha\]得到$\mu$的置信区间,置信系数为 $1-\alpha$:
\[[\hat{\theta_1}, \hat{\theta_2}] = \left[{\bar{X} - \sigma u_{\alpha \over 2} \over \sqrt{n}}, {\bar{X}+\sigma u_{\alpha \over 2} \over \sqrt{n}}\right]\]4.4.3 大样本法
示例,某事件A在每次实验中发生的概率为p,做n次独立实验,以$Y_n$记A发生的次数。求p的$1-\alpha$置信区间。
设n比较大,另q=1-p,由中央极限定理可知,${Y_n-np \over \sqrt{npq} } \sim N(0,1)$,从而可以作为枢轴变量:
\[P\left(-u_{\alpha \over 2} \leq {Y_n-np \over \sqrt{npq}} \leq u_{\alpha \over 2} \right) = 1-\alpha\]确定样本量大小
示例,假设某种成分含量服从$N(\mu,\sigma^2)$,其中$\sigma^2$已知,要求平均含量$\mu$的$1-\alpha$置信区间长度不能大于 w,求样本量大小。
由于$\sigma^2$已知,可以根据$\bar{X} \sim N(\mu, {\sigma^2 \over n})$构造$\mu$的95%置信区间,可知区间长度为 $2 u_{\alpha \over 2} {\sigma \over \sqrt{n}} \leq w$,从而可得:
\[n \geq \left( {2u_{\alpha \over 2} \sigma \over w} \right)^2\]第五章 假设检验
建立假设的原则:
- 将受保护的对象置为H0;
- 如果希望“证明”某个命题,取反命题作为H0(类似反证法)。