| 信号 | 分类 |
|---|---|
| 非周期性连续信号 | 傅立叶变换(Fourier Transform) |
| 周期性连续信号 | 傅立叶级数(Fourier Series) |
| 非周期性离散信号 | 离散时域傅立叶变换(Discrete Time Fourier Transform) |
| 周期性离散信号 | 离散傅立叶变换(Discrete Fourier Transform) |
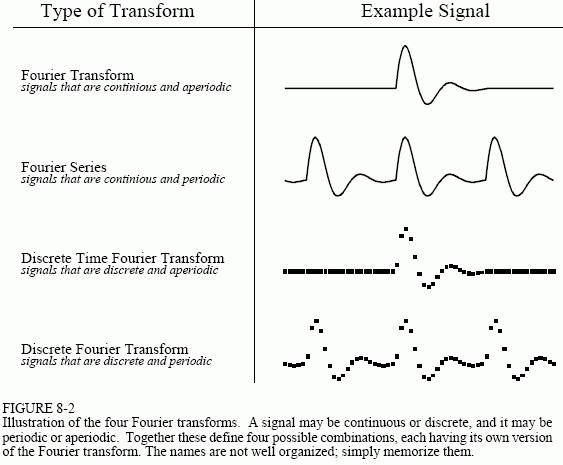
计算机因为只能处理离散信号,所以涉及到的是DFT。
傅立叶级数(Fourier Series)
\[S = \sum_{k=1}^n A_k\sin (2\pi kt+\phi_k)\]在数学中,傅里叶级数是一个可以把(有波形的)函数表示成多个简单的sin函数的叠加的方法。 更形式地说,傅里叶级数能够把任意周期函数(信号)分解成有限(或无限)个简单的震荡函数的叠加,这些震荡函数可以是正弦函数、余弦函数或复指数。
借助欧拉公式 $e^{ix} = \cos x + i\sin x$,傅立叶级数可以使用复指数来表示:
\[f(t) = \sum_{k=-n}^n c_k e^{2\pi ikt}\]其中,$c_k= \int _0^1 e^{-2\pi ikt }f(t)dt$ 就是傅立叶系数,参考 https://see.stanford.edu/materials/lsoftaee261/book-fall-07.pdf,第10-12页第1.5小节Lost at c的推导。
傅立叶变换(Fourier Transform)
参考:《复变函数与积分变换》华东理工大学出版社
时域和频域之间的转化。
函数 $f(t)$ 的傅立叶变换:
\[F(\omega ) = \int _{-\infty }^{+\infty }f(t)e^{-i\omega t}dt\]记作 $F(\omega ) = \mathcal {F}[f(t)]$,函数$F(\omega)$称做$f(t)$的像函数。
函数 $F(\omega)$ 的逆傅立叶变换:
\[f(t) = \frac {1}{2\pi }\int _{-\infty }^{+\infty }F(\omega )e^{i\omega t}d\omega\]记作 $f(t) = \mathcal {F}^{-1}[ F(\omega ) ]$,函数 $f(t)$ 称做 $F(\omega)$ 的像原函数。
傅立叶变换的性质:线性性质、位移性质、微分性质、积分性质、对称性质、相似性质。
离散傅立叶变换(Discrete Fourier Transform)
参考:Digital Signal Processing/Discrete Fourier Transform
设在时域上有离散的采样点 $f=(f[0],f[1],⋯,f[N−1])$,对$f$做DFT,可以得到频域上的离散点$F=(F[0],F[1],⋯,F[N−1])$,且
\[F[m] = \sum_{n=0}^{N-1}f[n]e^{-2\pi imn \over N}, m = 0,1,\dots ,N-1\]这就是DFT的标准公式。
其中,$f(t)$是原信号(时域),$f(n_0)$ 到 $f(n_{N−1})$ 是所谓的采样点,也就是说$f(t)$被离散成了这些点;$F(w)$ 是转换后的频域信号,$F(m_0)$ 到 $F(m_{N−1})$ 是频域里均匀分布的 $N$个点;那么上面的公式就是指,对于每个$m$值,都求出这$n$个采样点$f(n)$的傅里叶级数,这个级数就是$F(m)$。
示例:求解多项式乘法
两个n次多项式相乘,直接相乘时间复杂度为O(n^2),但利用FFT时间复杂度可以降到O(nlogn)。
次数界为$n$的多项式 $A(x)=\sum_{j=0}^{n-1} a_j x^j$,有两种表达方式:
- 系数表达:由系数组成的向量 $a=(a_0,a_1,\dots,a_{n-1})$,两个系数表达的多项式$a$和$b$相乘时间复杂度为$O(n^2)$,输出系数向量$c = a*b$ 是两者的卷积。
- 点值表达:由$n$个点值对组成的集合 $(x_0,y_0),(x_1,y_1),\dots,(x_{n-1},y_{n-1})$
显然,一个多项式只能有一种系数表达,但可以有很多种点值表达。从系数表达式推出点值表达式,称做求值;反过来,从点值表达求解出系数表达,称做插值。
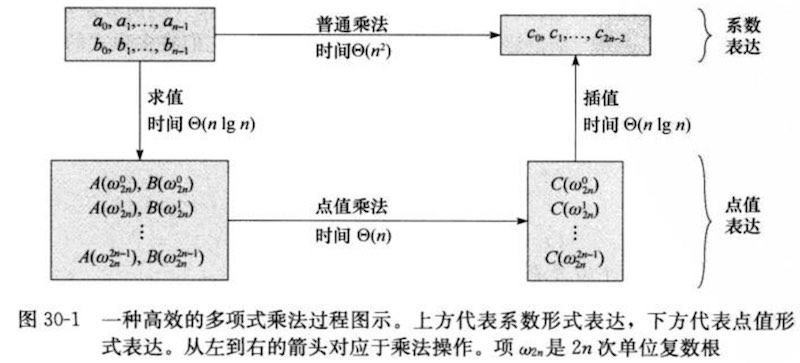
通过使用单位复数根(借助欧拉公式),FFT可以在 $O(n\log n)$ 时间复杂度内完成求值和插值计算。