概率分布汇总

Posted on |

[TOC]

描述离散型随机变量的概率分布使用 分布列。即给出离散型随机变量的全部取值，及取每个值的概率，明显概率和为1。

常见的离散型随机变量的分布有单点分布、两点分布、二项分布、几何分布、负二项分布、超几何分布、泊松分布等。

描述连续型随机变量的概率分布使用 密度函数（PDF） 和 分布函数（CDF）。

常见的连续型随机变量的分布有：均匀分布，正态分布、柯西分布、对数正态分布、指数分布、Gamma分布、Beta分布、卡方分布、学生分布、F分布等等。

把分布函数的概念推广到随机向量的情形，得到联合分布函数、边缘分布函数、联合分布列、边缘分布列、联合密度函数和边缘密度函数等概念。

特征函数 傅里叶变换是数学分布中非常重要而有用的工具，将它应用于概率论，对分布函数作傅里叶-斯蒂尔杰斯变换，就得到特征函数。特征函数与分布函数相互唯一决定，因而可以把求分布函数的问题转化为求特征函数的问题。

离散分布

0-1分布

伯努利分布 即 0-1分布 是对单次抛硬币的建模。

$X\sim \text{Bernoulli}(p)$的PDF为 \(f(x)=p^x (1−p)^{1−x}\)

其中，随机变量$X\in {0, 1}$。

二项分布

二项分布 是对多次抛硬币的建模。随机变量X的取值是出现正面的次数。二项分布有两个参数：抛的总次数$n$ 和 正面的概率 $p$。

$X\sim \text{Binomial}(n,p)$的PDF为

\[f(x)=P(X=x|n,p)={n \choose x} p^x (1−p)^{n−x}\]

【注】二项分布的极限是泊松分布。

多项分布

当$X$有多种取值时，如多次抛骰子，就应该用多项分布建模。这时参数$p$变成了一个向量 $p =(p_1,…,p_k)$ 表示X每一个取值被选中的概率。

$X\sim \text{Multinomial}(n,p)$ 的PDF为

\[f(x)=P(x_1, …, x_k|n,p )={n \choose 1, …, x_k}p_1^{x_1}…p_k^{x_k}={n! \over \prod_{i=1}^k x_i!} \prod_{i=1}^k p_i^{x_i}\]

几何分布

概率为p的事件A，X记作A首次发生所进行的试验次数，则X的分布列：

\[P(X=k) = (1-p)^{k-1} p, \qquad k=1,2,3,\dots\]

具有这种分布列的随机变量X，称为服从参数p的几何分布，记为$X\sim \text{Geo}(p)$。

\[E[X]=\frac1p,\qquad Var(X)=\frac{1-p}{p^2}\]

Poisson分布

泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。

\[P(k{\text{ events in interval}})=e^{-\lambda }{\frac {\lambda ^{k}}{k!}}\]

泊松分布的参数λ是单位时间内随机事件的平均发生率。泊松分布适合于描述单位时间内随机事件发生的次数。

\[E(X)=\lambda,\qquad Var(X)=\lambda\]

可以从各项同性推导出正态分布，从独立增量性推出泊松分布。

举例：我们去每天食堂打饭，在一段时间 t（比如 1 个小时）内来到食堂就餐的学生数量肯定不会是一个常数（比如一直是 200 人），而应该符合某种随机规律：比如在 1 个小时内来 200 个学生的概率是 10%，来 180 个学生的概率是 20%……一般认为，这种随机规律服从的就是泊松分布。

也就是在单位时间内有 k 个学生到达的概率为： \(P_k=\frac{\lambda^k}{k!}e^{-\lambda}\) 其中 λ 为单位时间内学生的期望到达数。

和二项分布

二项分布和泊松分布最大的不同是前者的研究对象是 n 个离散的事件（10 次射击），而后者考察的是一段连续的时间（单位时间）。因此泊松分布就是在二项分布的基础上化零为整。

当试验的次数趋于无穷大，而乘积 np 固定时，二项分布收敛于泊松分布。

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中λ为np。通常当n≧10,p≦0.1时，就可以用泊松公式近似得计算。

从二项分布可以推导出泊松分布。

和Gamma分布

Gamma分布pdf参数取$\alpha=k+1$得到

\[\text{Gamma}(x|\alpha=k+1) = \frac{x^ke^{-x}}{\Gamma(k+1)} = \frac{x^ke^{-x}}{k!}\]

和Poisson分布pdf的数学形式一致，可以直观认为Gamma分布是Poisson分布在正实数集上的连续版本。

二项分布可以把Gamma分布和Poisson分布联系起来，详见靳志辉的《LDA数学八卦：神奇的Gamma函数》。

和指数分布

泊松分布表示的是事件发生的次数，“次数”这个是离散变量，所以泊松分布是离散随机变量的分布。

\[P(N(t)=n) = \frac{(\lambda t)^n e^{-\lambda t}}{n!}\]

泊松分布更完整的表达方式，其中N(t)=n，表示时间t内发生了n次事件。

指数分布表示的是两件事情发生的平均间隔时间，“时间”是连续变量，所以指数分布是一种连续随机变量的分布。

\[P(X>t)=P(N(t)=0) = \frac{(\lambda t)^0e^{-\lambda t}}{0!} = e^{-\lambda t}\]

如上，指数分布可以用泊松分布推导出来，两个事件发生的平均间隔时间，表明时间t内没有事件发生，即N(t)=0。

一句话总结：泊松分布是单位时间内独立事件发生次数的概率分布，指数分布是独立事件的时间间隔的概率分布。

可以用等公交车作为例子：

某个公交站台一个小时内出现了的公交车的数量，就用泊松分布来表示。 某个公交站台任意两辆公交车出现的间隔时间，就用指数分布来表示。

泊松过程

编程产生符合泊松分布的随机数，即泊松过程。

  1. 从$\text{Uniform}(0,1)$的均匀分布出发，用 Inverse CDF 方法产生一系列独立的指数分布（参数为λ）随机数 $X_i \sim \exp(\lambda)$；
  2. 记$Y=X_1+X_2+\cdots+X_k$。如果$Y>t$，则停止，输出$k-1$；若否，则继续生成，直到$Y>t$为止；
  3. 重复步骤2。

容易证明，输出的一系列整数$k$ 就满足服从参数为$\mu=\lambda t$ 的Poisson分布。

Python代码：

def poisson(mu):
    y = k = 0
    while y <= 1:
        u = random.random()
        x = cmath.exp(-mu * u)
        y += x.real
        k += 1
    return k

参考：从 $uniform(1)$ 产生任意分布

连续分布

Gamma分布

Gamma函数

\[\Gamma(x) = \int_0^\infty t^{x-1}e^{-t}dt\]

Gamma函数的递归性质

\[\Gamma(x+1) = x\Gamma(x)\]

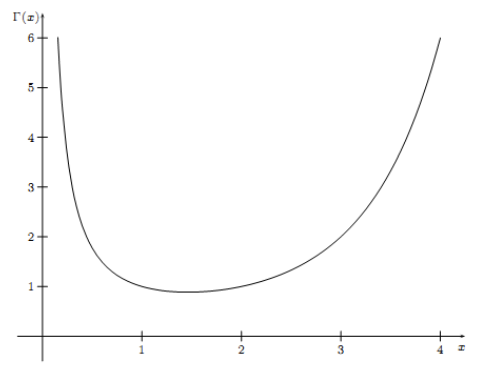
Gamma函数是阶乘在实数集上的推广，对整数有 $\Gamma(n)=(n-1)!$。 gamma distribution

Gamma分布的一般形式

\[\text{Gamma}(t|\alpha,\beta)={\beta^\alpha t^{\alpha-1} e^{-\beta t} \over \Gamma(\alpha)}\]

其中，$\alpha$称为shape parameter，主要决定分布曲线的形状；$\beta$称为rate parameter，主要决定曲线有多陡。

指数分布、$\chi^2$分布都是特殊的Gamma分布。

参考：怎么理解Gamma分布？

Beta分布

区别于随机变量的概率分布，Beta分布是概率的概率分布，即当我们不清楚某概率分布的情况下，描述该概率可能的取值情况。

直白的说，Beta分布是融合了先验的二项分布（参数$\alpha$和$\beta$对应随机变量取0和1的先验次数）。二项分布为后验分布，Beta分布为先验分布，而且由于它们函数形式相同，也称Beta分布是二项分布的共轭先验分布。

\[f(x) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}\]

均值和方差

\[E(X)=\frac\alpha{\alpha+\beta},\qquad Var(X)=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}\]

Beta 分布背后的含义

举例：我们做一个抛硬币实验，估算硬币正面向上的概率$\pi$。我们假设$\pi$的先验满足 $p(\pi)=\text{Beta}(\alpha,\beta)$

  • 每观察到一次正面向上：$p(\pi\vert X=1)=\text{Beta}(\alpha+1,\beta)$
  • 每观察到一次反面向上：$p(\pi\vert X=0)=\text{Beta}(\alpha,\beta+1)$

假设观察到正面向上81次，反面向上219次，则$\hat{\pi}=81/(81+219)=0.27$。

指数分布

$X\sim \text{Exponential}(\lambda)$ 表示间隔时间 t 之内随机事件没有发生的概率（可以从 Poisson 分布推导出来）：

\[P(X>t) = e^{-\lambda t}\]

反过来，事件在间隔时间 t 内发生的概率：

\[P(X\le t) = 1-e^{-\lambda t}\]

和幂律分布

幂律分布比指数分布更加长尾，如Pareto 分布。

正态分布

正态分布的概率密度函数均值为 μ 方差为σ2 (或标准差σ)是高斯函数的一个实例：

\[f(x; \mu,\sigma) = \frac{1}{\sigma \sqrt{2 \pi} } \exp \left(- {(x- \mu)^2 \over 2\sigma^2} \right)\]

卡方分布

设随机变量 $X_1,X_2,\dots,X_n$互相独立，且$X_i(i=1,2,\dots,n) \sim N(0,1)$，则它们的平方和 $\sum_{i=1}^n X_i^2$ 服从自由度为n的$\chi^2$分布。

自由度 是统计学中常用的一个概念，它可以解释为独立变量的个数，还可与解释为二次型的秩。

例如： $Y=X^2$是自由度为1的$\chi^2$分布，$rank(Y)=1$；$Z=\sum_{i=1}^nX_i^2$ 是自由度为n的 $\chi^2$ 分布，$rank(Z)=n$。

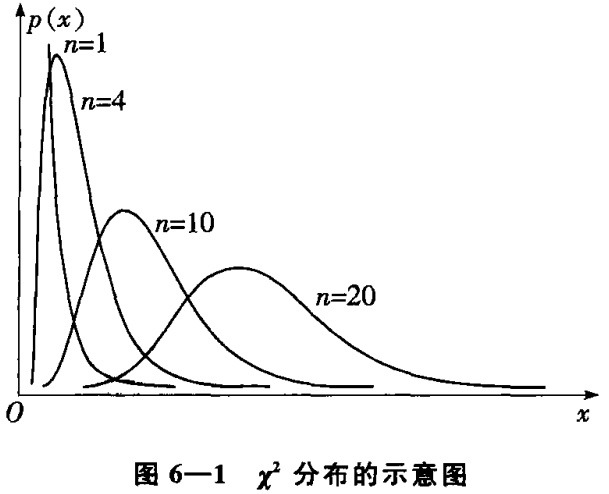
$\chi^2$分布的PDF曲线： Chi^2 dist

\[E(\chi^2) = n \\ D(\chi^2) = 2n \\ \chi_1^2+\chi_2^2 \sim\chi^2(n_1+n_2)\]

当 $n \to +\infty$ 时，$\chi^2$分布的极限是正态分布。

t分布

t分布也称Student分布，在小样本有重要作用（t-test）。

设随机变量 $X \sim N(0,1)$，$Y \sim \chi^2(n)$，且X与Y独立，则 $t={X \over \sqrt{Y/n}}$ ，其分布称为t分布t(n)，其中n是其自由度。

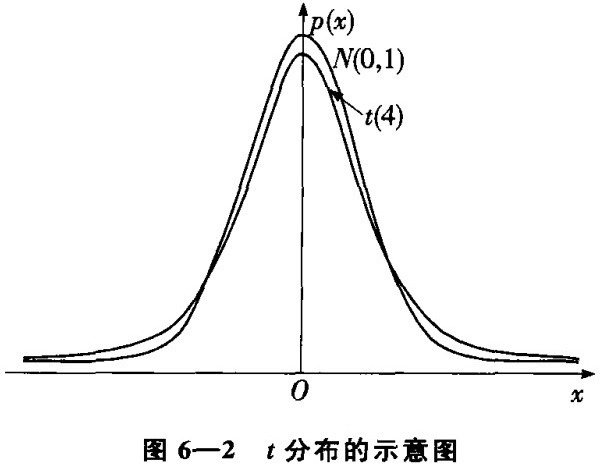
t分布的密度函数是一偶函数： t dist

\[E(t) = 0, \text{if}\quad n\ge 2 \\ D(t) = \frac{n}{n-2}, \text{if } n\ge 3\]

自由度为1的t分布称作柯西分布。

F分布

F分布在方差分析、回归方程的显著性检验中都有重要地位。

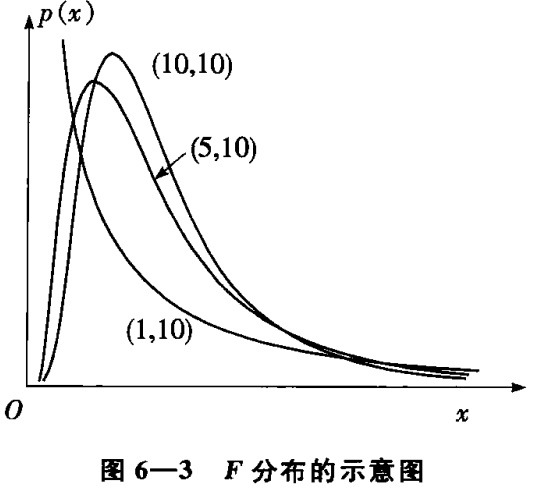
设随机变量Y和Z互相独立，且Y和Z分别服从自由度为m和n的$\chi^2$分布，随机变量 $X={Y/m \over Z/n}=\frac{nY}{mZ}$，则称X服从第一自由度为m，第二自由度为n的F分布，记为 $X \sim F(m,n)$ 。 F dist

\[E(X) = {n \over n-2}, n \gt 2 \\ D(X) = {2n^2(m+n-2) \over m(n-2)(n-4) }, n \gt 4\]

与t分布的关系： 如果随机变量X服从t(n)分布，则$X^2$服从F(1,n)的F分布。