[TOC]
$\newcommand{\x}{\mathrm{x}}\newcommand{\y}{\mathrm{y}}$
概率密度函数(Probability density function)
PDF一般只用来描述连续随机变量,描述离散变量使用分布列。 对于离散随机变量,PDF即在各点的概率值。如翻硬币,假如翻正面概率0.4,反面0.6,则这个模型的PDF就是{0.4, 0.6}。
【注意】PDF的X轴是随机变量X的取值范围,但Y轴可以超过1(与离散随机变量PDF不同,因为只要保证在X的值域上积分为1)。
http://stats.stackexchange.com/questions/4220/can-a-probability-distribution-value-exceeding-1-be-ok
例如,Gamma分布Beta(1/2,1/10) 在0和1取值为正无穷。
累积分布函数((Cumulative) distribution function)
CDF表示随机变量小于或等于其某一个取值x的概率(之和)。
\[F_X(x) = P(X \leq x)\]示例,抛一枚均匀的硬币两次,设随机变量$X$表示出现正面的次数,那么 $P(X=0)=P(X=2)=1/4$,$P(X=1)=1/2$,于是$F(X=1)=P(X<=1)=P(X=0)+P(X=1)=3/4$,所以这个函数的曲线如下图:
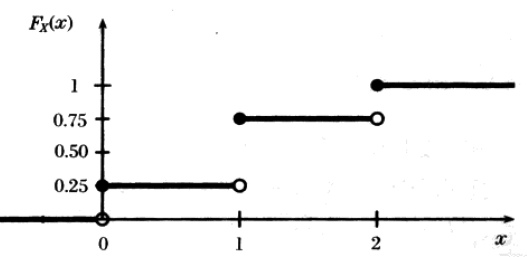
对于这个图,要想清楚清楚如下两个问题:
- 为什么函数始终是右连续的? 因为根据CDF的表达式中的小于等于号,当$X=x$时,$P(X=x)$的那部分应该被加到$F_X$上,因此在$X=x$处有一个值的跃升。如$X=1$时,$P(X=1)=1/2$
- 为什么$F_X(1.4)=3/4$? 要注意$P(1≤X<2)=1/2$(虽然其实$X$只能取整数值),但是$F_X$是值$x$之前所有概率的累加,所以$F_X(1.4)$可不是$1/2$,而是$3/4$ !!
因此CDF函数始终是非降的,右连续的,且 $\lim_{x\to \infty}F(x)=1$
期望 (均值)
一个离散性随机变量的期望值是试验中每次可能取值的概率乘以其取值的总和。
\[\bar{X} = \frac{ \sum_{i=1}^n X_i} {n}\]如果随机变量$X$的概率分布存在一个相应的概率密度函数$f(x)$,若积分$\int_{-\infty}^\infty x f(x) dx$ 绝对收敛,那么 $X$ 的期望值可以计算为: $E(X) = \int_{-\infty}^\infty xf(x) dx$
方差(Variance)
方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
\[s^2 = \frac{\sum_{i=1}^n (X_i - \bar{X})^2 } {n-1}\]标准差(Standard Deviation)
标准差,也称均方差(MSE,Mean Square Error),是方差的算术平方根。
\[s=\sqrt{ \frac{\sum_{i=1}^n (X_i - \bar{X})^2 } {n-1} }\]标准差反映一个数据集的离散程度。平均数相同的,标准差未必相同。
标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。 以这两个集合为例,[0,8,12,20]和[8,9,11,12],两个集合的均值都是10,但显然两个集合差别是很大的,计算两者的标准差,前者是8.3,后者是1.8,显然后者较为集中,故其标准差小一些,标准差描述的就是这种“散布度”。
标准差除以n-1而不是除以n,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。
协方差(Covariance)
协方差是方差的扩展,方差用来描述单个随机变量,而协方差可以用来描述两个随机变量的关系。
\[cov(X,Y) = {\sum_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y}) \over n-1}\]协方差意义:如果cov为正值,则说明两者是正相关的;如果cov为负值,则说明负相关的;如果cov为0,也是就是统计上说的“相互独立”。
- 皮尔逊相关系数(Pearson Correlation Coefficient)
- 可以用来判断两个变量的线性相关程度。
协方差矩阵
协方差只能描述两个随机变量的关系,而协方差矩阵用来更多随机变量之间的关系。
\[C=\left(\begin{matrix} cov(x,x) & cov(x,y) & cov(x,z) \\ cov(y,x) & cov(y,y) & cov(y,z) \\ cov(z,x) & cov(z,y) & cov(z,z) \end{matrix} \right)\]协方差矩阵是对称矩阵,矩阵对角线即是各随机变量的方差。
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差,而不是不同样本之间。 拿到一个样本矩阵,我们最先要明确的就是一行是一个样本还是一个维度。
概率公理
设$E$是随机试验,$\Omega$是它的样本空间,对于$\Omega$中的每一个事件$A$赋予一个实数,记为事件$A$的概率,集合函数$P(.)$满足下述三条公理:
- 公理1 $0\leq P(A) \leq 1$
- 公理2 $P(\Omega) = 1$
- 公理3 若事件 \(A_1,A_2,\cdots\) 两两互不相容,则有 \(P(A_1+A_2+\cdots)=P(A_1)+P(A_2)+\cdots\)
概率公式
- 乘法规则
- \[P(A\wedge B) = P(A\vert B)P(B) = P(B\vert A)P(A)\]
- 加法规则
- \[P(A\vee B) = P(A) +P(B) - P(A \wedge B)\]
- 贝叶斯法则
- \[P(A\vert B) = \frac{P(B\vert A) P(A) }{P(B)}\]
- 全概率法则
- 如果事件$A_1,\dots,A_n$互斥且$\sum_{i=1}^n P(A_i)=1$,则
- \[P(B) = \sum_{i=1}^n P(B\vert A_i) P(A_i)\]
条件概率
条件概率即事件y在事件x已经发生的条件下(given)的发生概率:
\[P(\y=y\vert \x=x) = {P(\y=y,\x=x) \over P(\x=x)}\]条件概率的链式法则(即乘法法则):
\[P(\x^{(1)},\dots,\x^{(n)}) = P\left(\x^{(1)}\right) \prod_{i=2}^nP\left(x^{(i)}\vert \x^{(1)},\dots,\x^{(i-1)}\right)\]示例:
\[\begin{array} \\ P(a,b,c) &=& P(a \vert b,c)P(b,c) \\ P(b,c) &=& P(b\vert c) P(c) \\ P(a,b,c) &=& P(a \vert b,c)P(b\vert c) P(c) \end{array}\]- 机器学习中的贝叶斯公式
- 由 $P(h\vert D) = P(D\vert h) \frac{P(h)}{P(D)}$ ,对于一个数据集下面的所有数据,可以认为P(D)是常数,于是 $P(h\vert D) \propto P(D\vert h) P(h)$,这个公式就是机器学习中的贝叶斯公式。
- 一般来说,我们称$P(h\vert D)$为模型的后验(posterior)概率,就是从数据来得到假设的概率;$P(h)$称为先验(prior)概率,就是假设空间的概率;$P(D\vert h)$是模型的likelihood概率。
边缘概率(Marginal probability)
已知一组变量的联合概率分布,其中一个子集的概率分布称作边缘概率分布。
假设有离散随机变量$\x$、$\y$,我们知道其联合概率分布$P(\x,\y)$,可以根据求和法则来计算$P(\x)$:
\[\forall x\in\x, P(\x=x)=\sum_y P(\x=x,\y=y)\]对连续变量:
\[p(x) = \int p(x,y) dy\]