Word2vec词向量

Posted on |

[TOC]

$\newcommand{\T}{\mathsf{T}}$

向量空间模型 (VSMs)将词汇表达（嵌套）于一个连续的向量空间中，语义近似的词汇被映射为相邻的数据点。向量空间模型在自然语言处理领域中有着漫长且丰富的历史，不过几乎所有利用这一模型的方法都依赖于 分布式假设，其核心思想为出现于上下文情景中的词汇都有相类似的语义。采用这一假设的研究方法大致分为以下两类：基于计数的方法 (e.g. 潜在语义分析)， 和 预测方法 (e.g. 神经概率化语言模型).

背景知识

统计语言模型（Statistical Language Model）是一种概率模型，它是NLP的基础，被广泛应用在语音识别、机器翻译、分词、词性标注和信息检索等任务。

假设句子$s:= (w_1,w_2,\cdots,w_T)$ 表示由这$T$个词按顺序构成，则该句子$s$的概率即是这些词的联合概率 $P(s)=p(w_1^T)=p(w_1,w_2,\cdots,w_T)$，这个概率分布也就是该语言的生成模型。利用Bayes公式，可以表示为各个词的条件概率形式 $P(s)=p(w_1)p(w_2\vert w_1)p(w_3\vert w_1^2)\cdots p(w_T\vert w_1^{T-1}) $，简写为

\[P(s)= \prod_{t=1}^T p(w_t|\text{Context}_t)\]

其中$\text{Context}_t$根据不同模型有不同的假设，具体有 n-gram、MaxEnt、HMM、CRF、NNLM、log-linear等方法。

n-gram模型

n-gram模型的基本假设，$n-1$阶Markov假设，认为一个词出现的概率只与它前面的$n-1$个词有关，即$p(w_t\vert w_1^{t-1})\approx p(w_t\vert w_{t-n+1}^{t-1})$，则有

\[\text{Contex}_t=w_{t-n+1}, w_{t-n+2},\cdots,w_{t-1}\]

其中，$n$表示往前看$n-1$个词，一般取值2或者3。优化目标函数是最大似然函数：

\[\mathcal{L}=\prod_{t=1}^T p(w_t|\text{Context}_t)\]

实际使用n-gram模型的时候，我们需要$p(w_t\vert \text{Context}_t)$，即元组n-gram到它概率的映射关系，这一般都需要离线统计并保存到内存里。n-gram数量巨大，超过trigram已经基本无法实际应用。如果可以用函数拟合出$p$，就有可能大幅减少n-gram参数数量，也就不用离线统计并占用巨大内存了，即：

\[p(w_t|\text{Context}_t) = f(w_t,\text{Context}_t;\theta)\]

拟合的函数有很多，线性的、非线性的，其中一种基于神经网络的方法NNLM，word2vec是它的变种。

NNLM

参考：Deep Learning in NLP （一）词向量和语言模型

Bengio 2001发表《A Neural Probabilistic Language Model》，提出NNLM，其中用到的重要工具即词向量（Distributed Representation）。

NNLM

目标是要学到一个好的模型：

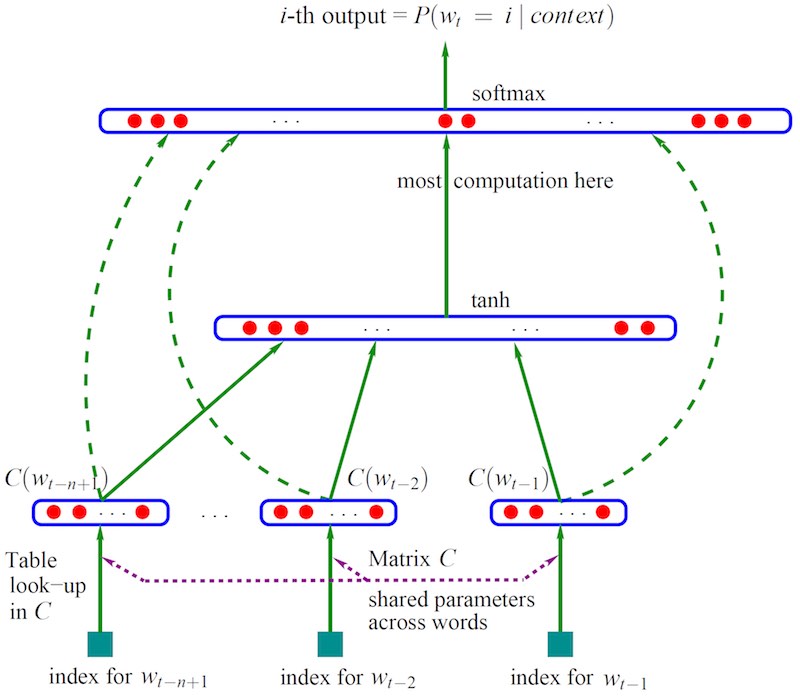
\[f(w_t^{t-n+1})=p(w_t|w_1^{t-1})\]

如图三层神经网络，$b,d,W,U,H,C$都是要计算的参数。

最下面的 $w_{t-n+1},\cdots, w_{t-2}, w_{t-1}$ 是前 $n-1$个词，即$\text{Context}_t$，以此预测下一个词 $w_t$。所以这是一个监督学习，样本是$(\text{Context}_t, w_t)$。 $C(w)$表示词$w$对应的词向量，整个模型中使用的是一套唯一的词向量，保存存在矩阵 $C$（一个 $\Abs{V}\times m$的矩阵）中。其中，$V$是全部语料的词汇，$m$是人为控制的词向量长度。

网络的第一层（输入层）是将$C(w_{t-1}),C(w_{t-2}),\cdots,C(w_{t-n+1})$这 $n−1$ 个向量依次concat起来，形成一个 $(n−1)m$ 维的向量，记为 $x$。参数$C$用于词向量的embedding，也是后续word2vec模型最重要的副产品。

\[x=\left(C(w_{t-1}),C(w_{t-2}),\cdots,C(w_{t-n+1})\right)\]

网络的第二层（隐藏层）就如同普通的神经网络，直接使用 $d+Hx$ 计算得到。在此之后，使用 $\tanh$ 作为激活函数。

网络的第三层（输出层）一共有 $\Abs{V}$ 个节点，每个节点 $y_i$ 表示 下一个词 $i$ 的未归一化 log 概率。$y$ 的计算公式为：

\[y=b+Wx+U\tanh(d+Hx)\]

其中，

  • $y$为$\Abs{V}$向量，是输出层；
  • $W$为$\Abs{V}\times (n-1)m$矩阵，是输入层直连到输出层的参数（实验中虽然不能提升模型效果，但可以减少迭代次数），如果不需要该连接，则参数$b$和$W$都可以置为0；
  • $U$为 $\Abs{V}\times h$ 矩阵，是隐藏层到输出层的参数；
  • $H$为 $h\times(n-1)m$ 矩阵，是输入层到隐藏蹭的参数。

整个模型的多数计算集中在 $U$ 和隐藏层的矩阵乘法中，后来的很多工作，都有对这一环节的简化，提升计算的速度。

最后，使用 softmax 激活函数将输出值 $y$ 归一化成概率。

\[p(w_t|w_{t-1}^{t-n+1}) = \frac{\exp(y_{w_t})}{\sum_i \exp(y_i)}\]

可以使用SGD优化。优化结束之后，词向量有了，语言模型也有了。

【注】《word2vec中的数学》为了和word2vec对应，采用四层结构，把这里的输入层$x$称作投影层。此外，前面还有一次table look-up，用来把one-hot的词 $w$ 转换为词向量，等价一次向量矩阵乘法：$C(w) = w \cdot C$

word2vec

Mikolov 2013提出word2vec论文：

  • Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word representations in vector space. Proceedings of ICLR. Retrieved from http://arxiv.org/abs/1301.3781
  • Mikolov, T., Sutskever, I., Chen, K., Corrado, G., & Dean, J. (2013). Distributed Representations of Words and Phrases and their Compositionality. arXiv:1310.4546 [Cs, Stat]. https://doi.org/10.1162/jmlr.2003.3.4-5.951

另外也可以参考（推荐，下文符号和截图均来自该论文）：

  • Rong, X. (2014). word2vec Parameter Learning Explained. arXiv:1411.2738 [Cs]. Retrieved from http://arxiv.org/abs/1411.2738

word2vec模型结构比Bengio提出的NNLM更简单，比如skip-gram只有两层。

  • 输入一组$\text{batch}$词；
  • 第一层embedding层参数$\Abs{V}\times m$，输出$\text{batch}\times m$；
  • 第二层输出层参数$\Abs{V}\times m$，输出$\text{batch}\times \Abs{V}$；
  • 然后softmax输出词的概率。

CBOW

根据上下文单词 $w_1,\cdots,w_C$（对应下图 $x_1,\cdots,x_C$），预测目标单词$w_O$（对应下图$y_j$），最大化该词出现的概率。

CBOW

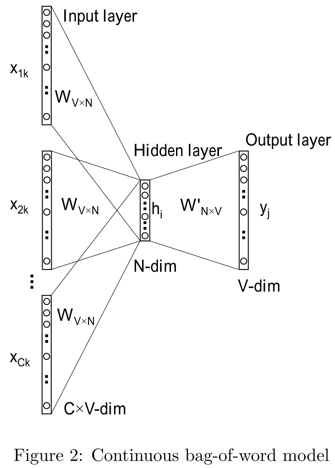
假设词表长度为$V$，词向量长度为$N$，涉及两个参数矩阵：

  • $W_{V\times N}$词向量矩阵，每行都是某个词的输入向量，记做$v$（词向量）
  • $W’_{N\times V}$矩阵，每列也是某个词的输出向量，记做$u$（Rong.X论文记做$v’$）

输入层$x$和输出层$y$都是词的one-hot编码，维度为$V$；中间层$h$，维度为$N$。

前向过程：

  • $x \to h$：将$x_i$乘以$W$得到输入向量$v_i$（即embedding_lookup），CBOW对这些向量累加取平均得到中间隐层$h=\frac1C(v_1+\cdots+v_C)$。
  • $h \to y$：将$h$乘以$W’$，得到score $s$（Rong.X论文记做$u$），然后softmax，取概率最大得到$y$。其中，$y_j$对应输出向量$u_j$，可以知道 $s_j={u_j}^T h$
\[\begin{aligned} y_j \leftarrow p(w_j|w_1,\cdots,w_C) &={\exp(s_j) \over \sum_{i=1}^V \exp(s_i)} \\ &={\exp\left(u_j^T h\right) \over \sum_{i=1}^V\exp\left(u_i^T h\right) } \end{aligned}\]

反向过程：

最小化loss函数：

\[\begin{aligned} \min J &= -\log p(w_j|w_1,\cdots,w_C) \\ &= -\log {\exp(s_j) \over \sum_{i=1}^V \exp(s_i)} \\ &= -u_j^Th +\log \sum_{i=1}^V\exp(u_i^Th) \\ \end{aligned}\]

具体推导过程见X.Rong的论文。最终得到$v$和$u$的更新公式。

1）$h\to y$ 更新$W’$，经过求导，$v’$的更新公式：

\[u_j^{(new)} = u_j^{(old)} - \eta (y_j-t_j) h, \quad j\in \{1,2,\cdots,V\}\]

其中，$t_j=1(j=j^*)$ 见论文公式$(8)$。 由于需要更新所有的$v’$向量，即整个$W’$矩阵，计算量很大。

2）$x\to h$ 更新$W$，经过求导，$v$的更新公式：

\[v_i^{(new)} = v_i^{(old)} - \frac1C\eta \sum_{j=1}^V (y_j-t_j) w'_{ij} ,\quad i=1,2,\cdots,C\]

最后一项实际是俩向量点乘。这里只需要更新$C$个上下文单词所对应的词向量。

Skip-gram

和CBOW反过来，根据单词$w_I$，预测上下文单词 $w_1,\cdots,w_C$，同样最大化这些词的出现概率。

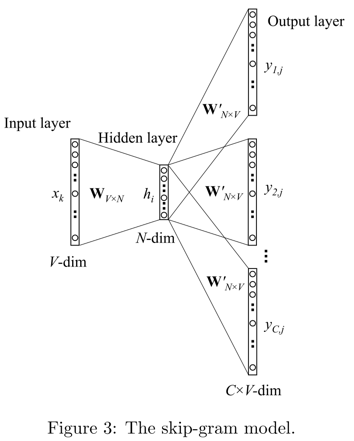
Skip-gram

最小化loss函数：

\[\begin{aligned} \min J &= -\log p(w_1,\cdots,w_C|w_I) \\ &= -\log \prod_{i=1}^C {\exp(s_i) \over \sum_{j=1}^V \exp(s_j)} \\ &= -\sum_{i=1}^Cu_i^Tv_I + C \cdot \sum_{j=1}^V\exp(u_j^Tv_I) \\ \end{aligned}\]

优化办法

原始方法的问题是计算量太大，主要是两个方面：

  • 前向过程，$h \to y$这部分在对向量进行softmax的时候，需要计算$V$次。
  • 后向过程，softmax涉及到了$V$列向量，所以也需要更新$V$个向量。

问题就出在$V$太大，而softmax需要进行$V$次操作，用整个$W$进行计算。

因此word2vec使用了两种优化方法，Hierarchical SoftMax和Negative Sampling，对softmax进行优化，不去计算整个$W$，大大提高了训练速度。

Hierarchical Softmax
利用Huffman编码，每个样本迭代在最后的softmax层由原来的O(N)次运算下降到了O(logN)级别。
Negative Sampling
不使用整个Vocabulary作为负例，负采样中词作为负样本的概率和其词频正相关，所以词频越高的越大概率被抽到。

评价指标

词向量的评价指标通常有以下几种：

  • 词汇相似度任务（similarity task），比如 WordSim353，但这种方式比较依赖于数据集。
  • 类比任务（analogy task），比如 vector(“Man”)-vector(“Woman”)=vector(“King”)-vector(“Queen”)。
  • 可视化，用PCA、t-SNE对高维词向量进行可视化，把数据降到三维或二维查看效果。
  • 应用于实际任务上的效果，比如 文本分类、情感分析、句法分析、序列标注、阅读理解等。

参考