反向传播(Back Propagation)是利用链式法则递归计算表达式的梯度的方法。
历史:1986年Rumelhart和Hinton一起重新发现了backprop,当时BP还是把求梯度和权重更新(梯度下降)打包了;而现在深度学习权重更新已经很简单粗暴了,BP基本单指第一步:求梯度。所以,现在BP已经完全等同于链式法则了。
图解传统BP 包括了前向传播+反向传播+更新权重。注意这里 $\delta$ 的含义有些混淆,没有乘以 $f’_i(e)$ ,可以结合这篇BP推导看,符号使用相对清晰。
思考:对DNN而言,单层网络(感知机)只要激活函数是单调的,能够保证是凸函数;但多层网络就是非凸优化了。
BP算法
Why:求解NN每层的参数,可以使用梯度下降,但难点在于如何计算每层loss对参数的梯度,而BP是计算梯度的有效方法。
BP算法推导参考Ufldl,损失函数为squared loss,激活函数为sigmoid,符号说明 如下:
- 样本集 $\brace{ (x^{(1)}, y^{(1)}), \ldots, (x^{(m)}, y^{(m)}) }$,包含$m$个样本。
- $W_{ij}^{(l)}$表示第 $l$ 层第 $j$ 单元与第 $l+1$ 层第 $i$ 单元之间的联接参数,
- $b^{(l)}_i$ 表示第 $l+1$ 层第 $i$ 单元的偏置项,
- $a^{(l)}_i$ 表示第 $l$ 层第 $i$ 单元的激活值(输出值),
- $z^{(l)}_i$ 表示第 $l$ 层第 $i$ 单元输入加权和(包括偏置单元)。
可知,\(z^{(l)}_i=\sum_j W_{ij}^{(l-1)}x_j +b_i^{(l-1)}\),则 \(a_i^{(l)}=f(z_i^{(l)})\)。
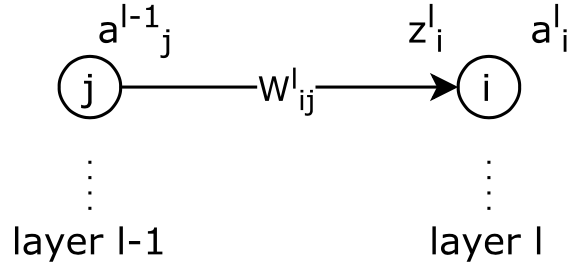
神经网络的参数是neuron之间的边,一组neuron组成layer。
SGD求解:
\[\begin{aligned} W_{ij}^{(l)} &= W_{ij}^{(l)} - \alpha \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) \\ b_{i}^{(l)} &= b_{i}^{(l)} - \alpha \frac{\partial}{\partial b_{i}^{(l)}} J(W,b) \end{aligned} \tag 1\]对单个样本$(x,y)$的loss,Ufldl里选择用squared loss,实际也可以使用logloss、交叉熵损失等:
\[J(W,b; x,y) = \frac{1}{2} \Abs{h_{W,b}(x) - y}^2.\]BP就是一个复合函数对每个参数求偏导(链式法则)的过程,补充一下Ufldl里缺失的步骤:
\[\begin{aligned} \frac{\partial J(W,b)}{\partial W_{ij}^{(l)}} &= \frac{\partial J}{\partial z_i^{(l)}} \cdot \frac{\partial z_i^{(l)}}{\partial W_{ij}^{(l)}} \\ &= \delta_i^{(l)} \cdot a_j^{(l-1)} \end{aligned} \tag 2\]其他推导步骤参考Ufldl即可:
输出层$n_l$残差(error term):
\[\begin{aligned} \delta^{(n_l)}_i &= \frac{\partial}{\partial z^{(n_l)}_i} \frac{1}{2} \Abs{y - h_{W,b}(x)}^2 \\ & = - (y_i - a^{(n_l)}_i) \cdot f'(z^{(n_l)}_i) \end{aligned} \tag 3\]中间层$l$残差:
\[\delta^{(l)}_i = \left( \sum_{j=1}^{s_{l+1}} W^{(l)}_{ji} \delta^{(l+1)}_j \right) f'(z^{(l)}_i) \tag 4\]逐层反向求解即为BP。其中,激活函数$f(z)$是sigmoid函数,则$f’(z^{(l)}_i) = a^{(l)}_i (1- a^{(l)}_i)$。实际也可以使用tanh、ReLU等。
代码示例
利用numpy手动实现前馈神经网络和反向传播算法,参考这里编写一个单隐层的神经网络:
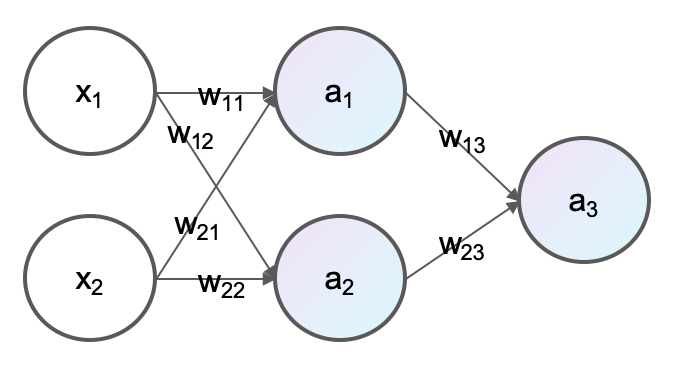
输入层维度3,中间隐层维度4,输出维度1的MLP,相当于两个参数矩阵($3\times 4$和$4\times 1$) 相乘。python代码如下:
import numpy as np
def nonlin(x,deriv=False):
if(deriv==True): return x*(1-x)
return 1/(1+np.exp(-x))
X = np.array([[0,0,1],
[0,1,1],
[1,0,1],
[1,1,1]])
y = np.array([[0,1,1,0]]).T
np.random.seed(1)
# 以均值0随机初始化参数矩阵
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1
for j in xrange(60000):
# (1) 前向传播 l0 -> l1 -> l2
l0 = X
l1 = nonlin(np.dot(l0,syn0))
l2 = nonlin(np.dot(l1,syn1))
# (2) 反向传播
## 计算输出层l2 error
l2_error = y - l2
if (j% 10000) == 0:
print "Error:" + str(np.mean(np.abs(l2_error)))
## 输出层残差:参考公式3
l2_delta = l2_error*nonlin(l2,deriv=True)
## 计算中间层l1每个参数对于输出层l2 error的贡献
l1_error = l2_delta.dot(syn1.T)
## 中间层残差:参考公式4
l1_delta = l1_error * nonlin(l1,deriv=True)
## 更新参数:参考公式1和2(SGD这里省略了学习率)
syn1 += l1.T.dot(l2_delta)
syn0 += l0.T.dot(l1_delta)